Analysis of LeetCode High Frequency Problems I

详细讲解LeetCode考察较多的3道题目：03、04、23。

3.Longest Substring Without Repeating Characters(无重复字符的最长子串)(Mid)

Given a string, find the length of the longest substring without repeating characters.

Example 1:

1
2
3

Input: "abcabcbb"
Output: 3 
Explanation: The answer is "abc", with the length of 3.

Example 2:

1
2
3

Input: "bbbbb"
Output: 1
Explanation: The answer is "b", with the length of 1.

Example 3:

Input: "pwwkew"
Output: 3
Explanation: The answer is "wke", with the length of 3. 
             Note that the answer must be a substring, "pwke" is a subsequence and not a substring.

解：解法一：暴力法

找到所有子串，然后每一个子串都一个一个地去判断是否有重复的字符。

要分析这个方法的时间复杂度，首先我们需要弄清楚一些问题，假设字符串长度为n，那么它有多少个非空子串？

答案是 n*(n+1)/2 个。

怎么计算出来的？

长度为1的子串，有n个
长度为2的子串，有n-1个
长度为3的子串，有n-2个

…

长度为k的子串，有n-k+1个
当k=n时，n-k+1=1，即长度为n的子串就是1个

所有情况相加，可以得到：
n+(n-1)+(n-2)+(n-3)+…+2+1 = n(n+1)/2
算上空字符串，一共有：(n(n+1)/2) + 1

在这里可以进行对比，子串和子序列的区别。比如，对于长度为n的字符串，一共有多少子序列？

答案是2^n

怎么计算得到的？

子序列不同于子串
子序列中的元素不需要相互挨着
长度为1的子序列有n个，即：C(1,n)
长度为2的子序列有C(2,n)个
长度为3的子序列有C(3,n)个

…

长度为k的子序列有C(k,n)个
所有子序列的个数(包括空序列)为：C(0,n) + C(1,n) + C(2,n) + C(3,n) + … + C(n,n) = 2^n

这里有关统计字符串的子串和子序列的过程和方法，和结果，务必熟悉和记下来，对于分析各种问题能有帮助。

如果对所有的子串进行判断，从每个子串里寻找最长且没有重复字符的，复杂度为：O(n* (n+1)/2 * n) = O(n^3)

当然，这不是最好的办法。

解法二：线性法

把每次遍历到的字符放入到一个哈希集合中，这样每次判断当前遍历过的内容中是否包含下一个要遍历的字符的时候，用哈希表的contains方法，时间复杂度为O(1),比不放到哈希表中的O(n)的速度能够得到提高。

具体解法：

定义一个哈希集合set
从给定字符串的头开始，每次检查当前字符是否在集合内。如果不在，说明该字符不会造成冲突和重复，将其加入到集合中，并统计当前集合长度，或许为最长子串

如果出现了重复的子串，处理方法是定义两个指针，i为慢指针，j为快指针。

当 j 遇到一个重复出现的字符时，我们从慢指针开始一个一个地将 i 指针指向的字符从集合中删除，然后判断是否可以把新字符加入到集合而不会重复。

class Solution {
    public int lengthOfLongestSubstring(String s) {
        // 定义一个哈希集合set,初始化结果max为0
        Set<Character> set = new HashSet<>();
        int max = 0;
        
        // 利用快慢指针i(慢)和j(快)扫描一遍字符串
        for(int i = 0, j = 0; j < s.length(); j++) {
            // 如果快指针指向的字符已经出现在哈希集合中,不断尝试将慢指针指向的字符从哈希集合中删除
            while(set.contains(s.charAt(j))) {
                set.remove(s.charAt(i));
                i++;
            }
            
            // 当快指针的字符终于能加入到哈希集合的时候，更新结果max
            set.add(s.charAt(j));
            max = Math.max(max, set.size());
        }
        // 遍历完毕后，返回结果max
        return max;
    }
}

时间复杂度分析：O(n)。使用了快慢指针策略，字符串最多被遍历两次。快指针会被添加到哈希表集合，慢指针遇到的字符会从哈希集合中删除。哈希集合操作时间为O(1)，因此整个算法复杂度为：n * O(1) + n*O(1) = O(n)
空间复杂度分析：O(n)。由于使用到哈希集合，最坏的情况下，即给定的字符串没有任何重复的字符，我们需要把每个字符都加入集合。

解法三：优化的线性法

基于方法二的线性法。也就是，如果我们在遍历过程中遇到了set已经有的字符的时候，如何不让慢指针一步一步移动，而是直接移动到重复元素的后面呢？这样可以大大减少比较次数。

这样一来我们需要能够记录每个字符出现的下标位置，可以用哈希表记录，因为查找过程时间复杂度也是O(1)

而且此时，我们不能像之前一样去数哈希集合的元素作为max的结果。比如可能出现一种情况，就是当前快指针j遍历到的元素在之前已经出现过了，那么此时不能让i又跳回到前面去呀！所以i的值需要有max计算得到：i = Math.max(i, map.get(s.charAt(j) + 1));

class Solution {
    public int lengthOfLongestSubstring(String s) {
        // 定义一个哈希表map用来记录上次某字符出现的位置,初始化结果max为0
        Map<Character, Integer> map = new HashMap<>();
        int max = 0;
        
        // 利用快慢指针i(慢)和j(快)扫描一遍字符串
        for(int i = 0, j = 0; j < s.length(); j++) {
            // 如果发现快指针所对应的字符已经出现过，慢指针就进行跳跃
            if(map.containsKey(s.charAt(j))) {
                i = Math.max(i, map.get(s.charAt(j)) + 1);
            }
            
            // 把快指针所对应的字符添加到哈希表中，更新结果max
            map.put(s.charAt(j), j);
            max = Math.max(max, j - i + 1);
        }
        // 遍历完毕后，返回结果max
        return max;
    }
}

4.Median of Two Sorted Arrays(寻找两个有序数组的中位数)(Hard)

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

You may assume nums1 and nums2 cannot be both empty.

Example 1:

nums1 = [1, 3]
nums2 = [2]

The median is 2.0

Example 2:

nums1 = [1, 2]
nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5

解：

油管上有关这道题的非常好的讲解：“Median of two sorted Arrays”: A Google Software Engineering Interview Question PART 1

解法一：暴力法

利用归并排序的思想将它们合并成一个长度为m+n的有序数组
合并的时间复杂度为 m+n，从中选取中位数

代码：

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int[] mergedArray = mergeTwoSortedArray(nums1,nums2);
        int n = mergedArray.length;
        // 先排好序，再返回中位数
        if(n % 2 == 0) {
            //若排好序的数组为偶数个，则取中间两个的平均数
            return (mergedArray[(n-1) / 2] + mergedArray[n/2]) / 2.0;
        } else {
            //总元素个数为奇数个，则选取中间那个
            return mergedArray[n/2];
        }
    }
    
    public int[] mergeTwoSortedArray(int[] nums1,int[] nums2) {
        int[] merged = new int[nums1.length + nums2.length];
        int i = 0, j = 0, k = 0;
        //两个array同时扫描
        while(i < nums1.length && j < nums2.length) {
            merged[k++] = nums1[i] < nums2[j] ? nums1[i++] : nums2[j++];
        }
        while(i < nums1.length) {
            merged[k++] = nums1[i++];
        }
        while(j < nums2.length) {
            merged[k++] = nums2[j++];
        }
        return merged;
    }
}

整体时间复杂度为O(m+n)，要大于题目要求的O(log(m+n))，不符合要求
空间复杂度：O(m+n)

可以自然地想到要用Binary Search

解法二：切分法，比较偏重数学

这种方法需要考虑m+n为奇数还是偶数。假设m+n=L，

如果L为奇数，即两个数组元素总个数为奇数，则中位数为第：int(L/2)+1小的数。
如果L为偶数，则中位数为第 int(L/2) 小于int(L/2)+1小的数求和的平均值。

所以我们的问题转变成了，在两个有序数组中寻找第k小的数，f(k)

当L为奇数时，若令 k=L/2，则结果为f(k+1)
当L为偶数时，结果为：(f(k) + f(k+1))/2

那么接下来的问题是，怎么从两个排好序的数组中找到第k小的数呢？

假设nums1[] = {a0, a1, a2, a3, a4}、nums2[] = {b0, b1, b2, b3}
举例，如果从nums1和nums2中分别取出k1和k2个元素：

a2=b1，这种算是最舒服的情况了,此时a2或者b1就是我们要找的第k小的数。因为此时我们如果把a0, a1, a2, b0, b1按照大小顺序合并在一起，那么a2和b1肯定排在最后，a0, a1 和b0都排在前面，不需要考虑这三个的大小关系。
a2<b1，这种情况开始不舒服了，我们无法肯定a2和b1是第五小的数。但是这种情况下我们可以确定，第五小的数一定不会是a0, a1, a2中的一个，同时也不会是b2和b3中的一个。所以，整个的搜索范围可以缩小为：{a3, a4, b0, b1}
a2>b1，我们同样无法肯定a2和b1是第五小的数。但是这种情况下我们可以确定，第五小的数不可能是b0, b1和a3, a4。所以这种情况下，整个搜索范围可以缩小为：{a0, a1, a2, b2, b3}

代码：

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        // 根据两个字符串长度的总和判断如何调用递归函数以及返回结果
        int m = nums1.length, n = nums2.length;
        
        int k = (m + n) >> 1;
        
        
        if((m+n) % 2 == 1) {
            // 当总长度为奇数时，返回正中间的数
            return findKth(nums1, 0, m-1, nums2, 0, n-1, k+1);
        } else {
            // 当总长度为偶数时，返回两个数的平均值
            return (findKth(nums1, 0, m-1, nums2, 0, n-1, k) + 
                    findKth(nums1, 0, m-1, nums2, 0, n-1, k+1)) / 2;
        }
    }
    
    // 进入findKth,这个函数目的是寻找第k小的元素
    public double findKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k) {
        int m = end1 - start1 + 1;
        int n = end2 - start2 + 1;
        
        // 如果nums1数组的长度大于nums2数组的长度，将二者互换，加快程序结束的速度
        if(m > n) {
            return findKth(nums2, start2, end2, nums1, start1, end1, k);
        }
        
        // 当nums1数组长度为0的时候，直接返回nums2数组中第k小的数
        if(m == 0) {
            return nums2[start2 + k - 1];
        }
        
        // 当k == 1时，返回两个数组中的最小值
        if(k == 1) {
            return Math.min(nums1[start1], nums2[start2]);
        }
        
        // 分别选两个数组的中间数
        int na = Math.min(k/2, m);
        int nb = k - na;
        int va = nums1[start1 + na -1];
        int vb = nums2[start2 + nb -1];
        
        // 比较下两者的大小
        // 如果相等，表明中位数已经找到，返回该值即可
        if(va == vb) {
            return va;
            // 如果不相等，进行剪枝处理
        } else if(va < vb) {
            return findKth(nums1, start1 + na, end1, nums2,start2,  start2 + nb - 1, k - na);
        } else {
            return findKth(nums1, start1, start1 + na - 1, nums2, start2 + nb, end2, k - nb);
        }
    }
}

解法三：二分查找

首先，我们需要利用两个数组已经是有序的这么一个性质，从A和B这两个数组中找到分割点，那么剩下的数字个数就是符合二分查找的数字数量。

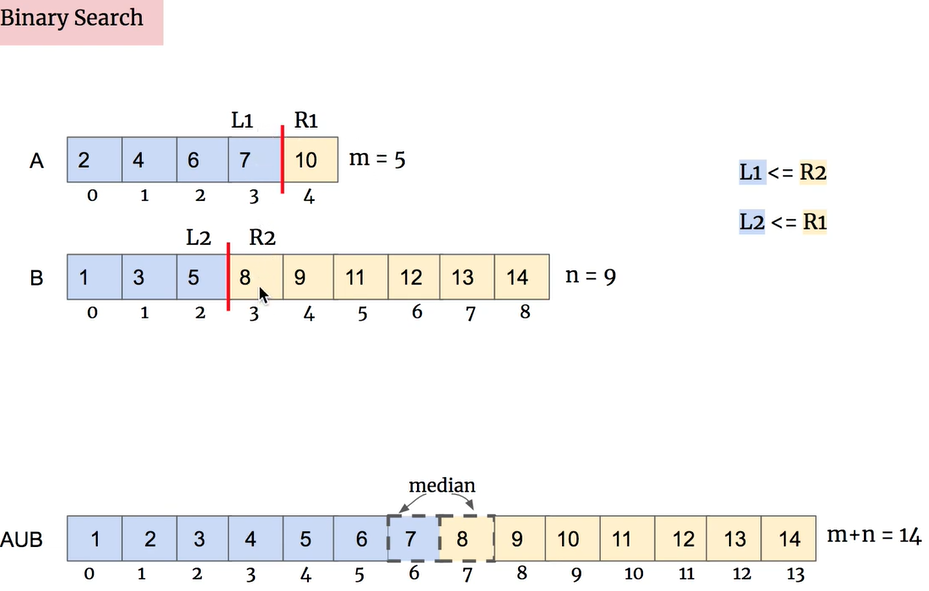
我们需要把握住一个特质：分割完之后，我们需要让A和B两个数组符合这个要求：A的分割点左边数组的最大值要小于B的分割点右边的最小值，而且B的分割点左边数组的最大值要小于A的分割点右边的最小值(这个条件很至关重要，满足了这个条件，就算找到了目标分割线。)。样例如下图：

因为题目提到了要求时间复杂度小于O(log(m+n))一下，所以自然想到二分查找。

class Solution {
    public double findMedianSortedArrays(int[] A, int[] B) {
        int lenA = A.length, lenB = B.length;
        //如果A不是较短的，则交换位置。因为下面的操作默认A是较短的数组
        //为什么选较短的？——选短的，二分查找也能更快。
        if(lenA > lenB) {
            return findMedianSortedArrays(B,A);
        }
        //特殊情况，如果A和B中短的数组是空的，那么直接返回另一个数组的中位数即可
        if(lenA == 0) {
            return ((double) B[(lenB - 1) / 2] + (double) B[lenB / 2]) / 2;
        }
        //新数组总长度为len
        int len = lenA + lenB;
        //上面已经提到，整个过程只对数组A进行binary search，所以只定义A的Start和End来维护
        //每次binary search的范围
        int AStartK = 0, AEndK = lenA;
        // cutA记录数组分割的左边元素个数、cutB记录分割的左边元素个数
        int cutA, cutB;
        while(AStartK <= AEndK) {
            cutA = (AStartK + AEndK) / 2;
            cutB = len / 2 - cutA;
            //L1=Integer.MIN_VALUE和L2=Integer.MIN_VALUE这两种情况肯定是不同时出现的，这样在后面Math.max(L1, L2)那里就可以让另外一个不等于Integer.MIN_VALUE的稳定当选
            double L1 = (cutA == 0) ? Integer.MIN_VALUE : A[cutA - 1];
            double L2 = (cutB == 0) ? Integer.MIN_VALUE : B[cutB - 1];
            //R1和R2同理
            double R1 = (cutA == lenA) ? Integer.MAX_VALUE : A[cutA];
            double R2 = (cutB == lenB) ? Integer.MAX_VALUE : B[cutB];
            if(L1 > R2) {
                AEndK = cutA - 1;
            } else if(L2 > R1) {
                AStartK = cutA + 1;
            } else {
                if(len % 2 == 0) { //如果合并之后数组元素个数为偶数
                    //则要取L1和L2的最大值与R1、R2的最小值的平均数
                    return (Math.max(L1, L2) + Math.min(R1,R2)) / 2;
                } else {
                    //如果合并后元素个数为奇数，则直接在L1和L2中更小的即可
                    return Math.min(R1,R2);
                }
            }
        }
        return -1;
    }
}

时间复杂度：O(logm)，m为较短的数组的长度
空间复杂度：O(1)

23.Merge k Sorted Lists(合并K个排序链表)(Hard)

Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity.

Example:

Input:
[
  1->4->5,
  1->3->4,
  2->6
]
Output: 1->1->2->3->4->4->5->6

解：解法一：暴力法

用一个数组保存所有链表中的数，之后进行排序，再从头到尾将数组遍历，生成一个排好序的链表
假设每个链表平均长度为n,整体时间复杂度为O(nk * log(nk))，偏大

解法二：最小堆

每次比较k个链表头，时间复杂度为O(k)
对k个链表头创建一个大小为k的最小堆
- 创建一个大小为k的最小堆所需时间为O(k)
- 从堆中取最小的数，所需时间都是O(logk)
- 如果每个链表平均长度为n，则共有nk个元素，即用大小为k的最小堆过滤nk个元素
- 整体时间复杂度为O(nk*log(k))
- 空间复杂度为O(k)，我们有k个list，占据k个空间

我们一直维护这个大小为k的最小堆，直到遍历完所有链表的节点

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */


class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        // 如果输入为[]，边界条件
        if(lists.length == 0 || lists == null) return null;
        
        // 利用一个空的链表头方便我们插入节点
        ListNode fakeHead = new ListNode(0), p = fakeHead;
        
        // 定义一个最小堆来保存k个链表节点
        int k = lists.length;
        
        // 将k个链表的头放到最小堆中,因为使用ListNode数据结构，所以重新定义比较器
        PriorityQueue<ListNode> heap = new PriorityQueue<>(k, new Comparator<ListNode>() {
            public int compare(ListNode a, ListNode b) {
                return a.val - b.val;
            }
        });
        
        // 从k个链表中将当前最小节点取出，插入到结果链表中
        // 每条链表都会有一个指针i，这个for把每条链表的第一个加入到小顶堆中
        // 因为本身就有k个链表，所以相当于初始化的步骤
        for(int i = 0; i < k; i++) {
            if(lists[i] != null) {
                heap.offer(lists[i]);
            }
        }
        
        // 真正使用最小堆的操作，将堆中元素一个一个取出，插入到结果链表中
        while(!heap.isEmpty()) {
            ListNode node = heap.poll();
            
            p.next = node;
            p = p.next;
            
            // p是结果链表节点，node是当前遍历的节点
            // 如果当前链表有后续节点，在poll()了它之后自然要访问它后续节点
            if(node.next != null) {
                heap.offer(node.next);
            }
        }
        
        // 最后返回结果链表
        return fakeHead.next;
    }
}

上述定义小顶堆的代码也可以用Lambda表达式简化：

1
2
3

PriorityQueue<ListNode> heap = new PriorityQueue<>(
    (a,b) -> a.val - b.val
);

解法三：分治法

利用分治思想，非常类似归并排序操作。

// 主函数非常类似归并排序的过程
public ListNode mergeKLists(ListNode[] lists, int low, int high) {
    // 如果输入为[]，边界条件
    if(lists.length == 0 || lists == null) return null;
    
    if(low == high) return lists[low];
    
    // 从中间切一刀
    int middle = low + (high - low) / 2;
    
    // 递归地处理坐标和右边的列表，最后合并起来
    return mergeTwoLists(
        mergeKLists(lists, low, middle),
        mergeKLists(lists, middle + 1, high)
    );
}

public ListNode mergeTwoLists(ListNode a, ListNode b) {
    if (a == null) return b;
    if (b == null) return a;
    
    if(a.val <= b.val) {
        a.next = mergeTwoLists(a.next, b);
        return a;
    }
    
    b.next = mergeTwoLists(a, b.next);
    return b;
}

时间复杂度：O(nk * log(k))
空间复杂度：O(1)，可以直接在链表上进行操作