0%

LeetCode Search

Posted on Edited on In
Symbols count in article: 24k

轻财足以聚人，律己足以服人，量宽足以得人，身先足以率人。——陈继儒

LeetCode搜索相关题目，其解决思路和具体代码。内容也包括二分查找。

在树的章节中已经包括了很多有关DFS和BFS的题目，比如，非常经典和重要的，树的层次遍历(102)和树的一些遍历。之前重复的在这里先不再写了。

74. Search a 2D Matrix(搜索二维矩阵)(Mid)

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

  • Integers in each row are sorted from left to right.
  • The first integer of each row is greater than the last integer of the previous row.

Example 1:

1
2
3
4
5
6
7
8
Input:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 3
Output: true

Example 2:

1
2
3
4
5
6
7
8
Input:
matrix = [
  [1,   3,  5,  7],
  [10, 11, 16, 20],
  [23, 30, 34, 50]
]
target = 13
Output: false

解：这道题和下一道题几乎是兄弟模样，但是比240更简单，主要因为properties的第二条——他在保证了每一行为递增的之外，还保证下一行的第一个元素一定大于上一行的最后一个。

经典的二分查找的思想，把整个二维数组当成是一个排好序的数组对待即可。

需要注意的一个很有用的公式：

  • 把m*n的二维矩阵转换成一个数组：matrix[x][y] => array[x * n + y]
  • 把一个array转换成m*n的二维矩阵：array[x] => matrix[x/n][x%n]

抓住了上面这个转换机制，就抓住了关键

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        // corner case
        if(matrix == null || matrix.length == 0) return false;
        // start为开始的位置，end为当前终止的位置
        // rows为行数，cols为列数
        int start = 0, rows = matrix.length, cols = matrix[0].length;
        int end = rows * cols - 1;
        while(start <= end) {
            // 找到当前中间位置的元素mid
            int mid = (end + start) >> 1 ;
            
            // 最关键的是用start和end与二维矩阵matrix之间的转换公式
            // 二维矩阵转换中最重要的是列数，这个和定义二维数组的时候，可以没有
            // 行数，但是必须声明列数的道理是一样的
            if(matrix[mid / cols][mid % cols] == target) return true;
            
            // 如果当前mid比target小，那么target一定在mid右边，就要把start右移
            // vice versa
            if(matrix[mid / cols][mid % cols] < target) {
                start = mid + 1;
            } else {
                end = mid - 1;
            }
        }
        return false;
    }
}
  • 时间复杂度：标准的二分查找，时间复杂度为O(log(m*n))
  • 空间复杂度：O(1)

240. Search a 2D Matrix II(搜索二维矩阵)(Mid)

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

  • Integers in each row are sorted in ascending from left to right.
  • Integers in each column are sorted in ascending from top to bottom.

Example:

Consider the following matrix:

1
2
3
4
5
6
7
[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

Given target = 5, return true.

Given target = 20, return false.

解：和74的区别是，此题输入的数组下一行的首元素和上一行相比不是递增的，而是在行和列这两个方向上是递增的，这样一来解题思路和上一题就完全不同了。上一题因为存储方式和二维矩阵与数组的转换方式有吻合之处所以可以用二分法，这里也可以，但是没有上一题那么容易解了。

但是不难发现，因为在行和列这两个方向是递增的，所以右上角成为了突破口。右上角的元素如果大于target，那么再次查找target的时候可以排除之前的一列；如果右上角元素小于target，那么再次查找的时候可以排除之前元素的这一行。

写法一：从右上角开始突破。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        // corner case
        if(matrix == null || matrix.length == 0) return false;
        // 从右上角开始
        // start our pointer fron top-right
        int row = 0, col = matrix[0].length - 1;
        while(col >= 0 && row <= matrix.length - 1) {
            if(matrix[row][col] == target) { // found it
                return true;
            } else if(matrix[row][col] < target) {
                row++;
            } else {
                col--;
            }
        }
        return false;
    }
}

同理，其实从左下角开始也可以，可以把左下角当做搜索的突破口，若当前元素小于target，那么下次从当前元素的右边开始，剔除掉当前元素在的列；如果当前元素大于target,下次从当前元素上一个开始，剔除掉当前元素在的行。

写法二：从左下角开始突破

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        // corner case
        if(matrix == null || matrix.length == 0) return false;
        // 从左下角开始
        // start our pointer fron bottom-left
        int col = 0, row = matrix.length - 1;
        while(row >= 0 && col <= matrix[0].length - 1) {
            if(matrix[row][col] == target) return true; // found it
            
            if(matrix[row][col] < target) {
                col++;
            } else {
                row--;
            }
        }
        return false;
    }
}

  • 时间复杂度：O(m + n)。时间复杂度分析的关键是注意到在每次迭代（我们不返回 true）时，行或列都会精确地递减/递增一次。由于行只能减少 mm 次，而列只能增加 nn 次，因此在导致 while 循环终止之前，循环不能运行超过 n+mn+m 次。因为所有其他的工作都是常数，所以总的时间复杂度在矩阵维数之和中是线性的。

  • 空间复杂度：O(1)。因为这种方法都只需要处理几个指针，所以内存占用是恒定的。

127. Word Ladder(单词接龙)(Mid)

Given two words (beginWord and endWord), and a dictionary’s word list, find the length of shortest transformation sequence from beginWord to endWord, such that:

  1. Only one letter can be changed at a time.
  2. Each transformed word must exist in the word list. Note that beginWord is not a transformed word.

Note:

  • Return 0 if there is no such transformation sequence.
  • All words have the same length.
  • All words contain only lowercase alphabetic characters.
  • You may assume no duplicates in the word list.
  • You may assume beginWord and endWord are non-empty and are not the same.

Example 1:

1
2
3
4
5
6
7
8
9
Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]

Output: 5

Explanation: As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog",
return its length 5.

Example 2:

1
2
3
4
5
6
7
8
Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]

Output: 0

Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.

解：这道题是面试中经常会出现的问题。一般思路，可以使用初级搜索，即单向BFS。但是这里着重介绍使用双向BFS的方法，从beginWord和endWord中更小的那个开始扩散。为什么这样扩散比单向扩散效率更高？

因为同时从beginWord和endWord开始，然后每次从更短的一段开始继续搜索，那么因为是更小的Set，所以辐射的内容会更少，如果需要剪枝或者回溯，代价也可以更小。

比如，打仗的时候一方总会派出侦察兵，这些侦察兵往往身上负重很轻，因为这样他们才可以移动迅速，累赘小。而如果他们被抓了，需要被放弃，那么少量的武器，也能成为更小的损失和代价。

实际上，双向BFS是属于高级搜索的范畴的。对于初级搜索(BFS和DFS)，一般来说优化的思路有两个：一是让搜索过程去掉重复以及尽早剪枝，二是让它在搜索方向上加强。

事实上，双向BFS在高级搜索中用得比较多，而且代码并不难。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
class Solution {
    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
        
        if(!wordList.contains(endWord)) return 0;
        
        // 用Set代替Queue进行BFS, 是为了更方便查询单词是否在wordList中
        // 如果不用哈希，直接的list查询时间复杂度为O(n),使用Set之后时间复杂度为O(1)
        Set<String> wordListSet = new HashSet<>(wordList);
        
        // beginSet是从beginWord开始扩散的，endSet是从endWord开始扩散的
        Set<String> beginSet = new HashSet<>(), endSet = new HashSet<>();
        
        // 这里和单向BFS中一开始往queue中加入元素的操作类似,加入初始元素
        // 可以看出，beginSet和endSet本质没有先后顺序,先扩散小的可以更快收敛
        beginSet.add(beginWord);
        endSet.add(endWord);
        
        // 转换次数，这是细节，由于beingWord != endWord, 所以至少一步
        int len = 1;
        
        // visited 表示这个BFS节点是否已经被访问过了
        Set<String> visited = new HashSet<>();
        
        
        // BFS start here
        while( !beginSet.isEmpty() ) {
            // 扩散的时候优先选择小的Set
            // 如果beginSet更小，就扩散它
            // 否则如果beginSet更大，交换这两个Set,还是小的Set开始扩散
            // 核心：控制当前循环从哪个方向进行bfs；让begin指向size更小的集合，这样不会一直从一个方向BFS
            if(beginSet.size() > endSet.size()) {
                Set<String> set = beginSet;
                beginSet = endSet;
                endSet = set;
            }
            
            // neighbor 这个set表示每一次要扩散的set的内容
            Set<String> neighbor = new HashSet<>();
            // 模板中这里会开始控制次数的for循环，但这里的HashSet和模板的queue是一样的含义,只是更方便查找
            for(String word : beginSet) {
                // 对每一个单词，变化它的字符位
                char[] chs = word.toCharArray();
                // 用字母表遍历当前chs的每一个字母
                for(int i = 0; i < chs.length; i++) {
                    for(char c = 'a'; c <= 'z'; c++) {
                        // 保存chs的当前位置的字母
                        char old = chs[i];
                        // 然后替换成当前遍历到的字母表的字母
                        chs[i] = c;
                        // 转换回String，从而使用endSet中的contains方法
                        // 否则不能对char[]使用contains方法
                        String target = String.valueOf(chs);
                        
                        // 因为endSet是从endWord那边扩散过来的，如果我们替换过程中产生的target也在
                        // 这个Set里，说明从begin扩散过来的Set和从end扩散过来的set，在这里相交了
                        // 这个相交的word就是target
                        if(endSet.contains(target)) {
                            return len + 1;
                        }
                        
                        // 如果当时没找到target，则继续扩散其他的target,且把target追加到下一次
                        // 要扩散的set里面去，这里的neighbor set就是后面要扩散的set
                        if(!visited.contains(target) && wordListSet.contains(target)) {
                            neighbor.add(target);
                            // 标记target 为 visited, 表示访问过了
                            visited.add(target);
                        }
                        // 把单词本身还原
                        chs[i] = old;
                    }
                }
            }
            // 处理完beign中的元素之后，让begin指向begin中的元素的邻居
            beginSet = neighbor;
            // 路径长度++
            len ++;
        }
        // 没有转换的路径
        return 0;
    }
}

126. (单词接龙 II)(Hard)

433. Minimum Genetic Mutation(最小基因变化)(Mid)

A gene string can be represented by an 8-character long string, with choices from "A", "C", "G", "T".

Suppose we need to investigate about a mutation (mutation from “start” to “end”), where ONE mutation is defined as ONE single character changed in the gene string.

For example, "AACCGGTT" -> "AACCGGTA" is 1 mutation.

Also, there is a given gene “bank”, which records all the valid gene mutations. A gene must be in the bank to make it a valid gene string.

Now, given 3 things - start, end, bank, your task is to determine what is the minimum number of mutations needed to mutate from “start” to “end”. If there is no such a mutation, return -1.

Note:

  1. Starting point is assumed to be valid, so it might not be included in the bank.
  2. If multiple mutations are needed, all mutations during in the sequence must be valid.
  3. You may assume start and end string is not the same.

Exmaple 1:

1
2
3
4
5
start: "AACCGGTT"
end:   "AACCGGTA"
bank: ["AACCGGTA"]

return: 1

Example 2:

1
2
3
4
5
start: "AACCGGTT"
end:   "AAACGGTA"
bank: ["AACCGGTA", "AACCGCTA", "AAACGGTA"]

return: 2

Example 3:

1
2
3
4
5
start: "AAAAACCC"
end:   "AACCCCCC"
bank: ["AAAACCCC", "AAACCCCC", "AACCCCCC"]

return: 3

解：这道题实际和单词接龙属于一种类型的题目，都是通过BFS解决状态图搜索问题。

200. Number of Islands(岛屿数量)(Mid)

Given a 2d grid map of '1's (land) and '0's (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Example 1:

1
2
3
4
5
6
7
Input:
11110
11010
11000
00000

Output: 1

Example 2:

1
2
3
4
5
6
7
Input:
11000
11000
00100
00011

Output: 3

解：参考油管上Kevin大神的代码，思路非常清晰。

这道题在面试中经常会考到，主要思想是利用dfs，每碰到一个”1”，都将其周围的所有”1”击沉掉，也就是全部重新设置为0，然后总的岛屿数量加1，这样持续下去可以每次将一块岛击沉。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public int numIslands(char[][] grid) {
        // error checking
        if(grid == null || grid.length == 0) return 0;
       
        int numIslands = 0;
        for(int i = 0; i < grid.length; i++) {
            for(int j = 0; j < grid[i].length; j++) {
                if(grid[i][j] == '1') {
                    numIslands += dfs(grid, i, j);
                }
            }
        }
        return numIslands;
    }
    // 沉岛法,将i和j相邻的所有为1的点全部置为0
    public int dfs(char[][] grid, int i, int j) {
        // terminator，分别对应上下左右四个方向的超比边界情况
        if(i < 0 || i >= grid.length || j < 0 || j >= grid[i].length || grid[i][j] == '0')
            return 0;
        
        //sink
        grid[i][j] = '0';
        
        // down
        dfs(grid, i+1, j);
        // right
        dfs(grid, i, j+1);
        // up
        dfs(grid, i-1, j);
        // left
        dfs(grid, i, j-1);
        return 1;
    }
}

153. Find Minimum in Rotated Sorted Array(寻找旋转排序数组中的最小值)(Mid)

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

Find the minimum element.

You may assume no duplicate exists in the array.

Example 1:

1
2
Input: [3,4,5,1,2] 
Output: 1

Example 2:

1
2
Input: [4,5,6,7,0,1,2]
Output: 0

解：用二分搜索解决，在二分搜索的过程中，我们每次找到区间的中点，然后根据某些条件去决定去区间的左边还是右边继续搜索。

重点是数组已经被旋转过了，所以简单的二分搜索不可行。

通过分析可以发现，旋转之后的数组两头总会存在头部元素比尾部元素大的情况，直到到了之前旋转的元素才会变化，我们可以把这个地方成为变化点：

变化点

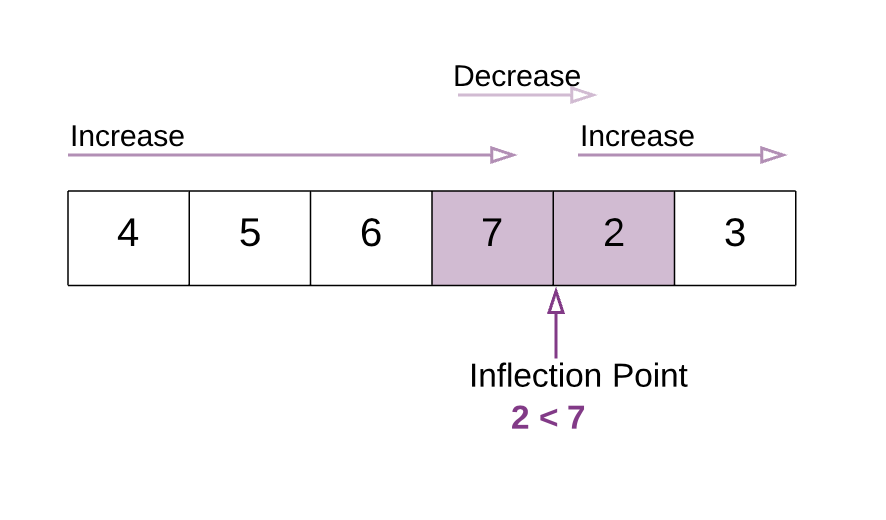
有关”变化点”的特点：

所有变化点左侧元素 > 数组第一个元素
所有变化点右侧元素 < 数组第一个元素

可以说这个是我们定义的新的”二分查找”

具体算法流程：

  1. 找到数组中间元素mid
  2. 如果中间元素 > 数组第一个元素，我们需要在mid右边搜索变化点
  3. 如果中间元素 < 数组第一个元素，我们需要在mid左边搜索变化点
  4. 当我们找到变化点时停止搜索，当以下条件满足任意一个即可：

  • nums[mid] > nums[mid + 1]，因此 mid+1 是最小值。

  • nums[mid - 1] > nums[mid]，因此 mid 是最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int findMin(int[] nums) {
        int len = nums.length;
        // corner case
        if(len == 1) return nums[0];
        
        int left = 0, right = len-1;
        if(nums[left] < nums[right]) return nums[0];
        
        // binary search
        while(right >= left) {
            int mid = (left + right) >> 1;
            
            if(nums[mid] > nums[mid + 1]) {
                return nums[mid + 1];
            }
            
            if(nums[mid] < nums[mid - 1]) {
                return nums[mid];
            }
            
            if(nums[mid] > nums[0]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
            
        }
        return -1;
    }
}

把代码简化一点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int findMin(int[] nums) {
        int len = nums.length;
        if(len == 0 || nums == null) {
            return -1;
        }
        
        int left = 0, right = len - 1;
        
        while(left < right) {
            int mid = (left + right) >> 1;
            if(mid > 0 && nums[mid] < nums[mid - 1]) {
                return nums[mid];
            }
            if(nums[left] <= nums[mid] && nums[mid] > nums[right]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        
        return nums[left];
    }
}
  • 时间复杂度：O(logN)，和二分搜索一样
  • 空间复杂度：O(1)

154. Find Minimum in Rotated Sorted Array(寻找旋转排序数组中的最小值 II)(Hard)

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

Find the minimum element.

The array may contain duplicates.

Example 1:

1
2
Input: [1,3,5]
Output: 1

Example 2:

1
2
Input: [2,2,2,0,1]
Output: 0

Note:

  • This is a follow up problem to Find Minimum in Rotated Sorted Array.
  • Would allow duplicates affect the run-time complexity? How and why?

写在前面：这可以算是代码最简单的Hard题之一。

这道题是上一题153的延伸题目，而且和剑指offer面试题11相同。(重点在于考虑可能会有重复元素)

解：注意这里只能用mid位置的值去和nums[right]去比较，不能用mid位置的值和nums[left]比较，因为做比较的目的是判断 mm 在哪个排序数组中。但在 numbers[m] > numbers[i]情况下，无法判断 m 在哪个排序数组中。本质是因为 j 初始值肯定在右排序数组中； i 初始值无法确定在哪个排序数组中。

举例：当 i = 0, j = 4, m = 2 时，有 numbers[m] > numbers[i] ，以下两示例得出不同结果。
numbers = [1, 2, 3, 4 ,5] 旋转点 x = 0 ： m 在右排序数组（此示例只有右排序数组）；
numbers = [3, 4, 5, 1 ,2]旋转点 x=3 ： m 在左排序数组。

所以循环比较nums[mid]和nums[right]

  1. 当 numbers[m] > numbers[j]时： m 一定在 左排序数组中，即旋转点 x 一定在 [m + 1, j] 闭区间内，因此执行 i = m + 1；
  2. 当 numbers[m] < numbers[j] 时： m 一定在 右排序数组 中，即旋转点 xx 一定在[i, m] 闭区间内，因此执行 j = m；
  3. 当 numbers[m] == numbers[j] 时： 无法判断 m 在哪个排序数组中，即无法判断旋转点 x 在 [i, m] 还是 [m + 1, j] 区间中。解决方案： 执行 j = j - 1缩小判断范围
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int findMin(int[] nums) {
        int len = nums.length;
        if(len == 0 || nums == null) return -1;
        
        int left = 0, right = len - 1;
        while(left < right) {
            int mid = (left + right) >> 1;
            if(nums[mid] > nums[right]) {
                left = mid + 1;
            } else if(nums[mid] < nums[right]){
                right = mid;
            } else {
                right--;
            }
        }
        return nums[left];
    }
}
  • 时间复杂度：O(logN),但是在特例下(比如所有元素都相等的情况)，会退化到O(N)
  • 空间复杂度：O(1),left,right,mid指针都是常数大小的空间

79. Word Search (单词搜索)(Mid)

Given a 2D board and a word, find if the word exists in the grid.

The word can be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example:

1
2
3
4
5
6
7
8
9
10
board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

Given word = "ABCCED", return true.
Given word = "SEE", return true.
Given word = "ABCB", return false.

Constraints:

  • board and word consists only of lowercase and uppercase English letters.
  • 1 <= board.length <= 200
  • 1 <= board[i].length <= 200
  • 1 <= word.length <= 10^3

解：这道题用递归或者叫回溯来解决。每次只要当前字符和word的第一个字母相同，就开始使用函数dfs进行DFS搜索，每次搜索的方向是上、下、左、右四个，只有找到了才返回true

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public boolean exist(char[][] board, String word) {
        
        if(word.length() == 0 || word == null) return true;
        
        for(int i = 0; i < board.length; i++) {
            for(int j = 0; j < board[i].length; j++) {
                if(board[i][j] == word.charAt(0) && dfs(board,i,j,0,word)) {
                    return true;
                }
            }
        }
        return false;
    }
    
    public boolean dfs(char[][] board,int i, int j, int count, String word) {
        if(count == word.length()) {
            return true;
        }
        // 处理边界条件，分别是:go above the board(处在边界上面，下同)(i < 0)、go below the board(i >= board.length)
        // go left the board(j < 0)、go right the board (j >= board[i].length)、
        // 或者就是当前字母不匹配word的单词：board[i][j] != word.charAt(count)
        if(i < 0 || i >= board.length || j < 0 || j >= board[i].length || board[i][j] != word.charAt(count)) {
            return false;
        }
        
        char temp = board[i][j]; // 记录当前i,j位置的字符
        board[i][j] = ' '; // 访问过的地方置空，防止重复访问
        
        boolean found = dfs(board,i+1,j,count+1,word)
            || dfs(board,i-1,j,count+1,word)
            || dfs(board,i,j+1,count+1,word)
            || dfs(board,i,j-1,count+1,word);
        // 因为之前每次查找的时候都清空了当前位置元素，所以再找的时候要把值赋回去。因为你不能确保第一次就找到，可能一个字母
        // 要在四个方向都各自查找一次才行，如果之前被置空了而且不管了，那么再找的时候其为空，那就无论如何也不可能找到了，就出错了
        board[i][j] = temp;
        return found;
    }
}
  • 时间复杂度：如果整个board元素数量是N,那时间复杂度就是O(N)
  • 空间复杂度：因为调用了递归，可能坏的情况是要每一个元素都建立一个变量，所以空间复杂度应该是O(n)

剑指offer面试题13.机器人的运动范围(Mid)

地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

示例1：

1
2
输入：m = 2, n = 3, k = 1
输出：3

示例2：

1
2
输入：m = 3, n = 1, k = 0
输出：1

提示：

  • 1 <= n,m <= 100
  • 0 <= k <= 20

解：这道题和上面的79单词搜索比较类似，都可以用DFS，或者叫回溯的思想。

DFS通过递归，先朝着一个防线搜索到底，再回溯至上一个节点，沿另一个方向搜索，以此类推。在访问过程中可以用到剪枝：遇到数位和超出目标值(k)、或者某位已经访问过，则立即返回，可以称之为可行性剪枝

具体做法：

  • 递归参数：可以把m,n,k定义到类外面成为类变量而不是方法变量来减少需要传入的参数值；要传入当前在矩阵中的索引i和j、记录某节点是否被访问过的visited
  • 终止条件：1.行或者列索引越界(和79机器人、200岛屿相同)、2.数位和si和sj的和超出目标值k、3.当前元素已经访问过
  • 递归工作：
    • 标记当前单元格为已访问，即将(i,j)存入Set visited中，代表此单元格已被访问过。
    • 搜索下一个单元格：计算当前元素的下、右两个方向元素的数位和，并开启下层递归。
  • 回溯返回值：返回 1 + 右方搜索的可达解总数 + 下方搜索的可达解总数，代表从本单元格递归搜索的可达解总数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    
    int m,n,k;
    
    public int movingCount(int m, int n, int k) {
        this.m = m;
        this.n = n;
        this.k = k;
        // visited记录当前位置是否被访问过
        boolean[][] visited = new boolean[m][n];
        return dfs(0, 0, visited);
    }
    public int dfs(int i, int j, boolean[][] visited) {
        // terminator
        if(add(i,j) > k || i < 0 || i >= m || j < 0 || j >= n || visited[i][j]) {
            return 0;
        }
        
        // 当前位置满足条件而且没被访问过，所以进行访问。
        // 访问之后将visited置true
        visited[i][j] = true;
        
        int result = 0;
        result = 1 + dfs(i + 1,j ,visited) + dfs(i ,j + 1 ,visited);
        return result;
    }
    
    private int add(int i, int j) {
        int result = 0;
        while(i != 0) {
            result += i%10;
            i /= 10;
        }
        while(j != 0) {
            result += j%10;
            j /= 10;
        }
        return result;
    }
}

17. Letter Combinations of a Phone Number(电话号码的字母组合)(Mid)

Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent.

A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.

Example:

1
2
Input: "23"
Output: ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

Note:
Although the above answer is in lexicographical order(字典序), your answer could be in any order you want.

解：这道题是比较经典的搜索问题。深搜和广搜都可以。

方法一：

994. Rotting Oranges (腐烂的橘子)(Mid)

In a given grid, each cell can have one of three values:

  • the value 0 representing an empty cell;
  • the value 1 representing a fresh orange;
  • the value 2 representing a rotten orange.

Every minute, any fresh orange that is adjacent (4-directionally) to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1 instead.

Example 1:

img

1
2
Input: [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

1
2
3
Input: [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation:  The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

1
2
3
Input: [[0,2]]
Output: 0
Explanation:  Since there are already no fresh oranges at minute 0, the answer is just 0.

Note:

  1. 1 <= grid.length <= 10
  2. 1 <= grid[0].length <= 10
  3. grid[i][j] is only 0, 1, or 2.

解：首先这道题应该用DFS还是BFS呢？

因为最后的结果可以理解是从腐烂的橘子开始向外扩散，每分钟向周围扩散一层，扩散完所有橘子所需要的最小时间。用BFS的思路可以很好契合，这是一个BFS的最短路径搜索问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
class Solution {
    public int orangesRotting(int[][] grid) {
        
        Queue<int[]> queue = new LinkedList<>();
        
        //count表示新鲜橘子的数量
        int count = 0;
        
        //遍历二维数组，找出所有新鲜橘子和腐烂的橘子
        for(int i = 0 ; i < grid.length; i++) {
            for(int j = 0; j < grid[i].length; j++) {
                //新鲜橘子计数
                if(grid[i][j] == 1) {
                    count++;
                } else if(grid[i][j] == 2) { //腐烂橘子放入queue开始BFS
                    queue.add(new int[]{i,j});
                }
            }
        }
        
        //round表示腐烂橘子的轮数，或者叫分钟数
        int round = 0;
        
        //如果有新鲜橘子，并且队列不为空，开始围绕队列中橘子开始遍历
        //直到上下左右都触及边界，或者被感染的橘子已经遍历完
        while(count > 0 && !queue.isEmpty()) {
            
            //BFS层数+1
            round++;
            
            //拿到当前层级腐烂橘子的数量，放在这里是因为每个层级
            //队列都会更新
            int n = queue.size();
            
            //遍历当前层级的队列
            for(int i = 0; i < n; i++) {
                //踢出队列，或者说是拿到一个腐烂的橘子
                int[] orange = queue.poll();
                
                //恢复橘子坐标
                int row = orange[0];
                int col = orange[1];
                
                //该橘子的上邻点，判断是否越界并且是否是健康的橘子
                if(row >= 1 && grid[row-1][col] == 1) {//是健康的橘子且不越界
                    //感染这个橘子
                    grid[row-1][col] = 2;
                    //好橘子的数量减1
                    count--;
                    //把感染的橘子放进队列，当做缓存，下次使用
                    queue.add(new int[]{row-1, col});
                }
                
                //该橘子的下邻点，和上面类似
                if(row < grid.length-1 && grid[row+1][col] == 1) {
                    grid[row+1][col] = 2;
                    count--;
                    queue.add(new int[]{row+1, col});
                }
                
                //该橘子的左邻点，和上面类似
                if(col >= 1 && grid[row][col-1] == 1) {
                    grid[row][col-1] = 2;
                    count--;
                    queue.add(new int[]{row, col-1});
                }
                //该橘子的右邻点，和上面类似
                if(col < grid[0].length-1 && grid[row][col+1] == 1) {
                    grid[row][col+1] = 2;
                    count--;
                    queue.add(new int[]{row, col+1});
                }
            }
        }
        //若遍历完了还存在新鲜的橘子，则返回-1
        //否则返回round
        if(count != 0) {
            return -1;
        } else {
            return round;
        }
    }
}

33. Search in Rotated Sorted Array (搜索旋转排序数组)(Mid)

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

You are given a target value to search. If found in the array return its index, otherwise return -1.

You may assume no duplicate exists in the array.

Your algorithm’s runtime complexity must be in the order of O(log n).

Example 1:

1
2
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Example 2:

1
2
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

解：二分查找进行旋转。利用”整个数组是部分有序”的这么一个特质。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 1. 暴力：还原O(logN) -> 升序 -> 二分:O(logN) (写、总结)，概括就是要用二分查找去找到数组汇总被某个元素劈断的位置
// 2. 正解：二分查找
class Solution {
    public int search(int[] nums, int target) {
        if(nums.length == 0) return -1;
        int low = 0, high = nums.length - 1;
        int mid;
        while(low <= high) {
            mid = (low + high) >> 1;
            if(nums[mid] == target) { //找到了
                return mid;
            }
            //前半部分有序,注意此处用小于等于
            if(nums[low] <= nums[mid]) {
                //target在前半部分
                if(target >= nums[low] && target < nums[mid]) {
                    high = mid - 1;
                } else {
                    low = mid + 1;
                }
            } else { //mid的前半部分无序
                if(target <= nums[high] && target > nums[mid]) {
                    low = mid + 1;
                } else {
                    high = mid - 1;
                }
            }
        }
        return -1;
    }
}

4.Median of Two Sorted Arrays(寻找两个有序数组的中位数)(Hard)

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

You may assume nums1 and nums2 cannot be both empty.

Example 1:

1
2
3
4
nums1 = [1, 3]
nums2 = [2]

The median is 2.0

Example 2:

1
2
3
4
nums1 = [1, 2]
nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5

解：

油管上有关这道题的非常好的讲解：“Median of two sorted Arrays”: A Google Software Engineering Interview Question PART 1

解法一：暴力法

  • 利用归并排序的思想将它们合并成一个长度为m+n的有序数组
  • 合并的时间复杂度为 m+n，从中选取中位数

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int[] mergedArray = mergeTwoSortedArray(nums1,nums2);
        int n = mergedArray.length;
        // 先排好序，再返回中位数
        if(n % 2 == 0) {
            //若排好序的数组为偶数个，则取中间两个的平均数
            return (mergedArray[(n-1) / 2] + mergedArray[n/2]) / 2.0;
        } else {
            //总元素个数为奇数个，则选取中间那个
            return mergedArray[n/2];
        }
    }
    
    public int[] mergeTwoSortedArray(int[] nums1,int[] nums2) {
        int[] merged = new int[nums1.length + nums2.length];
        int i = 0, j = 0, k = 0;
        //两个array同时扫描
        while(i < nums1.length && j < nums2.length) {
            merged[k++] = nums1[i] < nums2[j] ? nums1[i++] : nums2[j++];
        }
        while(i < nums1.length) {
            merged[k++] = nums1[i++];
        }
        while(j < nums2.length) {
            merged[k++] = nums2[j++];
        }
        return merged;
    }
}
  • 整体时间复杂度为O(m+n)，要大于题目要求的O(log(m+n))，不符合要求
  • 空间复杂度：O(m+n)

可以自然地想到要用Binary Search

解法二：切分法，比较偏重数学

这种方法需要考虑m+n为奇数还是偶数。假设m+n=L，

  • 如果L为奇数，即两个数组元素总个数为奇数，则中位数为第：int(L/2)+1小的数。
  • 如果L为偶数，则中位数为第 int(L/2) 小于int(L/2)+1小的数求和的平均值。

所以我们的问题转变成了，在两个有序数组中寻找第k小的数，f(k)

  • 当L为奇数时，若令 k=L/2，则结果为f(k+1)
  • 当L为偶数时，结果为：(f(k) + f(k+1))/2

那么接下来的问题是，怎么从两个排好序的数组中找到第k小的数呢？

假设nums1[] = {a0, a1, a2, a3, a4}、nums2[] = {b0, b1, b2, b3}
举例，如果从nums1和nums2中分别取出k1和k2个元素：

3iuZt0.png

  1. a2=b1，这种算是最舒服的情况了,此时a2或者b1就是我们要找的第k小的数。因为此时我们如果把a0, a1, a2, b0, b1按照大小顺序合并在一起，那么a2和b1肯定排在最后，a0, a1 和b0都排在前面，不需要考虑这三个的大小关系。
  2. a2<b1， 这种情况开始不舒服了，我们无法肯定a2和b1是第五小的数。但是这种情况下我们可以确定，第五小的数一定不会是a0, a1, a2中的一个，同时也不会是b2和b3中的一个。所以，整个的搜索范围可以缩小为：{a3, a4, b0, b1}
  3. a2>b1，我们同样无法肯定a2和b1是第五小的数。但是这种情况下我们可以确定，第五小的数不可能是b0, b1和a3, a4。所以这种情况下，整个搜索范围可以缩小为：{a0, a1, a2, b2, b3}

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        // 根据两个字符串长度的总和判断如何调用递归函数以及返回结果
        int m = nums1.length, n = nums2.length;
        
        int k = (m + n) >> 1;
        
        
        if((m+n) % 2 == 1) {
            // 当总长度为奇数时，返回正中间的数
            return findKth(nums1, 0, m-1, nums2, 0, n-1, k+1);
        } else {
            // 当总长度为偶数时，返回两个数的平均值
            return (findKth(nums1, 0, m-1, nums2, 0, n-1, k) + 
                    findKth(nums1, 0, m-1, nums2, 0, n-1, k+1)) / 2;
        }
    }
    
    // 进入findKth,这个函数目的是寻找第k小的元素
    public double findKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k) {
        int m = end1 - start1 + 1;
        int n = end2 - start2 + 1;
        
        // 如果nums1数组的长度大于nums2数组的长度，将二者互换，加快程序结束的速度
        if(m > n) {
            return findKth(nums2, start2, end2, nums1, start1, end1, k);
        }
        
        // 当nums1数组长度为0的时候，直接返回nums2数组中第k小的数
        if(m == 0) {
            return nums2[start2 + k - 1];
        }
        
        // 当k == 1时，返回两个数组中的最小值
        if(k == 1) {
            return Math.min(nums1[start1], nums2[start2]);
        }
        
        // 分别选两个数组的中间数
        int na = Math.min(k/2, m);
        int nb = k - na;
        int va = nums1[start1 + na -1];
        int vb = nums2[start2 + nb -1];
        
        // 比较下两者的大小
        // 如果相等，表明中位数已经找到，返回该值即可
        if(va == vb) {
            return va;
            // 如果不相等，进行剪枝处理
        } else if(va < vb) {
            return findKth(nums1, start1 + na, end1, nums2,start2,  start2 + nb - 1, k - na);
        } else {
            return findKth(nums1, start1, start1 + na - 1, nums2, start2 + nb, end2, k - nb);
        }
    }
}

解法三：二分查找

首先，我们需要利用两个数组已经是有序的这么一个性质，从A和B这两个数组中找到分割点，那么剩下的数字个数就是符合二分查找的数字数量。

我们需要把握住一个特质：分割完之后，我们需要让A和B两个数组符合这个要求：A的分割点左边数组的最大值要小于B的分割点右边的最小值，而且B的分割点左边数组的最大值要小于A的分割点右边的最小值(这个条件很至关重要，满足了这个条件，就算找到了目标分割线。)。样例如下图：

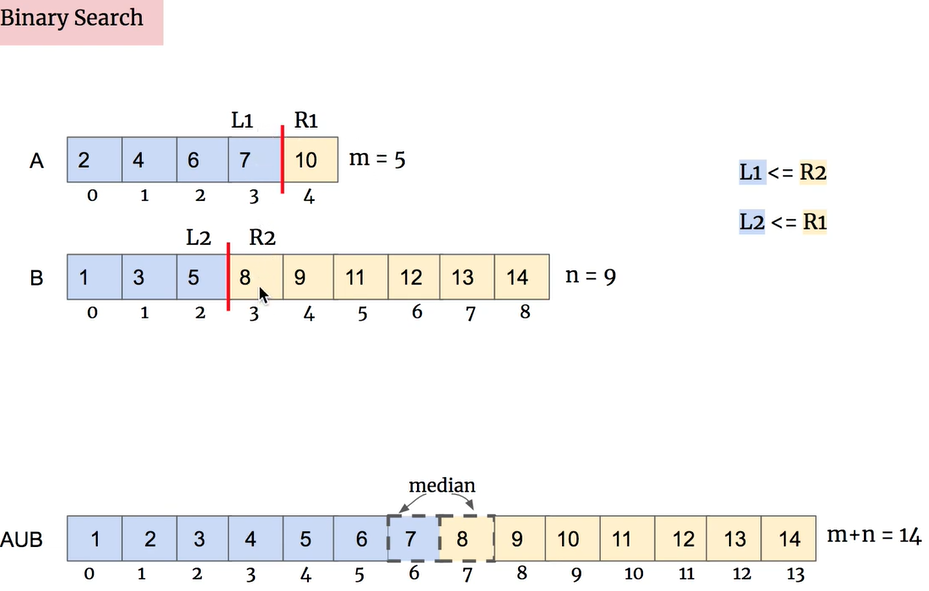
04题二分查找的示意图.png

因为题目提到了要求时间复杂度小于O(log(m+n))一下，所以自然想到二分查找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
    public double findMedianSortedArrays(int[] A, int[] B) {
        int lenA = A.length, lenB = B.length;
        //如果A不是较短的，则交换位置。因为下面的操作默认A是较短的数组
        //为什么选较短的？——选短的，二分查找也能更快。
        if(lenA > lenB) {
            return findMedianSortedArrays(B,A);
        }
        //特殊情况，如果A和B中短的数组是空的，那么直接返回另一个数组的中位数即可
        if(lenA == 0) {
            return ((double) B[(lenB - 1) / 2] + (double) B[lenB / 2]) / 2;
        }
        //新数组总长度为len
        int len = lenA + lenB;
        //上面已经提到，整个过程只对数组A进行binary search，所以只定义A的Start和End来维护
        //每次binary search的范围
        int AStartK = 0, AEndK = lenA;
        // cutA记录数组分割的左边元素个数、cutB记录分割的左边元素个数
        int cutA, cutB;
        while(AStartK <= AEndK) {
            cutA = (AStartK + AEndK) / 2;
            cutB = len / 2 - cutA;
            //L1=Integer.MIN_VALUE和L2=Integer.MIN_VALUE这两种情况肯定是不同时出现的，这样在后面Math.max(L1, L2)那里就可以让另外一个不等于Integer.MIN_VALUE的稳定当选
            double L1 = (cutA == 0) ? Integer.MIN_VALUE : A[cutA - 1];
            double L2 = (cutB == 0) ? Integer.MIN_VALUE : B[cutB - 1];
            //R1和R2同理
            double R1 = (cutA == lenA) ? Integer.MAX_VALUE : A[cutA];
            double R2 = (cutB == lenB) ? Integer.MAX_VALUE : B[cutB];
            if(L1 > R2) {
                AEndK = cutA - 1;
            } else if(L2 > R1) {
                AStartK = cutA + 1;
            } else {
                if(len % 2 == 0) { //如果合并之后数组元素个数为偶数
                    //则要取L1和L2的最大值与R1、R2的最小值的平均数
                    return (Math.max(L1, L2) + Math.min(R1,R2)) / 2;
                } else {
                    //如果合并后元素个数为奇数，则直接在L1和L2中更小的即可
                    return Math.min(R1,R2);
                }
            }
        }
        return -1;
    }
}
  • 时间复杂度：O(logm)，m为较短的数组的长度
  • 空间复杂度：O(1)