LeetCode Others

时间像海绵里的水，只要你愿意挤，总还是有的。——鲁迅

LeetCode其他题目其解决思路和具体代码。

169. Majority Element(多数元素)(Easy)

Given an array of size n, find the majority element. The majority element is the element that appears more than ⌊ n/2 ⌋ times.

You may assume that the array is non-empty and the majority element always exist in the array.

Example 1:

1 2	Input: [3,2,3] Output: 3

Example 2:

1 2	Input: [2,2,1,1,1,2,2] Output: 2

解：题目名字是”多数元素”，实际上，就是众数。

思路一：如果你头脑足够灵活，数学感觉足够好，那么实际上抓住一个点就可以：题目问的多数元素，其实不算真正的众数。这里的多数元素出现的次数必须大于 n/2 ，所以，如果一个数组中一定有众数，那么这个数组排好序之后，下标为 nums.length/2 的那个元素，就是众数。利用排序，排好序之后返回下标为 nums.length/2的元素，就是这道题需要的结果。

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length/2];
    }
}

因为用到了系统自带的排序方法，所以这种方法的时间复杂度是O(NlogN)。

方法二：开两个变量，result为最后返回的结果，count用于统计，因为按照题目定义，众数出现次数一定大于 n/2 ，所以count只要回到了0，说明当前result不可能是最后的众数。

class Solution {
    public int majorityElement(int[] nums) {
        int result = 0, count = 0;
        for(int num : nums) {
            if(count == 0) 
                result = num;
            if(result != num) 
                count --;
            else {
                count ++;
            }
        }
        return result;
    }
}

时间复杂度：O(n)
空间复杂度：O(1)

7. Reverse Integer(整数反转)(Mid)

Given a 32-bit signed integer, reverse digits of an integer.

Example 1:

1 2	Input: 123 Output: 321

Example 2:

1 2	Input: -123 Output: -321

Example 3:

1 2	Input: 120 Output: 21

Note:
Assume we are dealing with an environment which could only store integers within the 32-bit signed integer range: [−2^31, 2^31 − 1]. For the purpose of this problem, assume that your function returns 0 when the reversed integer overflows.

解：x最大可以取2^31-1，但是当x取最大值的时候，再reverse之后的数字大小会超出原本Integer能够保存的最大2^31-1的范围了，会报错移除。所以我们需要考虑到如何解决这个溢出的问题。

需要注意：1，翻转后的数字是否会溢出、2，有关负数的处理

如果不发生溢出，每次的当前结果可以得到是x0*10+y=x1，x1为计算之后得到的新的值。此时我们可以转换一下，解出来x的值：x=(x1-y)/10，可以想到，如果整个计算结果不发生溢出，这个式子是成立的。但是如果计算结果发生了溢出(比如到了2^31-1)，那么这个式子会不成立，我们可以通过这个方式检查当前数字反转之后是否会溢出。
比如传入的是-123，那么-123/10=-12，而且-123%10=-3，然后result*10+x%10这个公式实际上也是负数之间的计算，所以对于负数，不用单独考虑，就用一样的公式计算即可。

class Solution {
    public int reverse(int x) {
        int result = 0;
        while(x != 0) {
            // 用一个公式的正和反是否相等来判断当前数字是否溢出
            // result表示以前的数字，乘10再加上新来的数字即为翻转后的数newReverse
            int newReverse = result * 10 + x % 10;
            if((newReverse - x % 10) / 10 != result) return 0; // 溢出则返回0
            result = newReverse;
            x /= 10;
        }
        return result;
    }
}

9. Palindrome Number(回文数)(Mid)

Determine whether an integer is a palindrome. An integer is a palindrome when it reads the same backward as forward.

Example 1:

1 2	Input: 121 Output: true

Example 2:

1
2
3

Input: -121
Output: false
Explanation: From left to right, it reads -121. From right to left, it becomes 121-. Therefore it is not a palindrome.

Example 3:

1
2
3

Input: 10
Output: false
Explanation: Reads 01 from right to left. Therefore it is not a palindrome.

Follow up:

Coud you solve it without converting the integer to a string?

解：为了避免溢出问题(如果给的数字本身不是回文，翻转之后有可能大于int.MAX,造成溢出)，直接比较反转的int数的一半即可。

首先要处理临界情况，所有的负数都不可能是回文(这就可以过滤到很多啦！)。

后面的操作就是取出来数字了，取个位可以用对10取余，取十位可以用除以10之后再对10取余。

判断是否到了原始数字的一半，可以让原始数字除以10，再让反转后的数字乘上10。此时如果原始数字小于反转后的数字，就意味着我们已经处理了一半位数的数字了。

class Solution {
    public boolean isPalindrome(int x) {
        // 处理特殊情况
        // 所有负数都一定不是回文数
        // 如果某一个数字最后一位是0，那么如果它是回文数，
        // 那么开头也一定要是0，只有0符合
        if(x < 0 || (x % 10 == 0 && x != 0)) return false;
        
        int revertedNumber  = 0;
        while( x > revertedNumber ) {
            revertedNumber  = revertedNumber  * 10 + x % 10;
            x = x/10;
        }
        // 当数字长度为奇数时，我们可以通过 revertedNumber/10 去除处于中位的数字。
        // 例如，当输入为 12321 时，在 while 循环的末尾我们可以得到 x = 12，revertedNumber = 123，
        // 由于处于中位的数字不影响回文（它总是与自己相等），所以我们可以简单地将其去除。
        return (x == revertedNumber  || x == revertedNumber /10);
    }
}

时间复杂度：O(log10(N))，因为每次迭代，我们会将输入除以10，因此时间复杂度为O(log10(N))
空间复杂度：O(1)

1109. Corporate Flight Bookings(航班预订统计)(Mid)

There are n flights, and they are labeled from 1 to n.

We have a list of flight bookings. The i-th booking bookings[i] = [i, j, k] means that we booked k seats from flights labeled i to j inclusive.

Return an array answer of length n, representing the number of seats booked on each flight in order of their label.

Example 1:

1 2	Input: bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5 Output: [10,55,45,25,25]

Constraints:

1 <= bookings.length <= 20000
1 <= bookings[i][0] <= bookings[i][1] <= n <= 20000
1 <= bookings[i][2] <= 10000

解：这道题利用很经典的”上下车”的思路，可以把booking[i]=[i, j, k]理解成在i站上车k人，这些人乘坐到了第j站，然后在j+1站下车，我们要返回的是按照顺序的每一站上车的人数。

根据上面的思路，定义一个counter[]数组来记录每站人数的变化，counter[i]表示第i+1站。遍历bookings[],bookings[i]=[i,j,k]表示在i站增加k人,即counter[i-1] += k，在j+1站减少k人，即counter[j] -= k

最后遍历counter[]数组，得到每站的总人数：每站的总人数为前一站人数加上当前人数变化：counter[i] += counter[i-1]

重点：第i站上车、第j+1站下车。一开始counter只用于记录某一站人数的变化，后面counter用于保存每一站总共的人数。

class Solution {
    public int[] corpFlightBookings(int[][] bookings, int n) {
        // 需要注意：counter记录的是人数变化量
        int[] counter = new int[n];
        for(int[] booking : bookings) {
            // counter[i]表示第i-1站上车，上车人数是booking[2]
            counter[booking[0] - 1] += booking[2];
            if(booking[1] < n) { // 如果在最后一站或者最后一站之前下车，就要减去
                counter[booking[1]] -= booking[2];
            }
        }
        // 统计最后每一站的人数的结果
        for(int i = 1; i < n; i++) {
            counter[i] += counter[i - 1];
        }
        return counter;
    }
}

时间复杂度：O(n),n是航班的数量
空间复杂度：O(n)

135. Candy(分发糖果)(Hard)

There are N children standing in a line. Each child is assigned a rating value.

You are giving candies to these children subjected to the following requirements:

Each child must have at least one candy.
Children with a higher rating get more candies than their neighbors.

What is the minimum candies you must give?

Example 1:

1
2
3

Input: [1,0,2]
Output: 5
Explanation: You can allocate to the first, second and third child with 2, 1, 2 candies respectively.

Example 2:

Input: [1,2,2]
Output: 4
Explanation: You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
             The third child gets 1 candy because it satisfies the above two conditions.

解：需要注意题目说的是，评分高的children分到的candy是比他的neighbors多，而不是比其他所有评分比他低的小孩多

一个比较巧妙的方法是，可以从左往右和从右往左两次遍历，改变当前结果数组candy需要遵循这个公式：candy[i] = Math.max(candy[i],candy[i+1]+1)

class Solution {
    public int candy(int[] ratings) {
        if(ratings == null || ratings.length == 0) return 0;
        int len = ratings.length;
        // 最后的结果数组
        int[] result = new int[len];
        // 初始化每个小孩至少有一个糖果
        Arrays.fill(result, 1);
        // 然后开始遍历，一次从前往后，一次从后往前
        // 两次遍历的过程中第一个都不用管，因为在下一次遍历中会遍历到的
        
        // 从左往右,从第2个小孩开始直到最后一个
        for(int i = 1; i < len; i++) {
            // 如果当前小孩评分比他右边的小孩高，他分到的糖果数
            // 就比他右边的小孩多1个
            if(ratings[i] > ratings[i - 1]) {
                result[i] = result[i - 1] + 1;
            }
        }
        
        // 从右往左，从倒数第二个小孩开始直到第一个
        for(int i = len - 2; i >= 0; i--) {
            // 如果当前小孩评分比他左边小孩低，他左边小孩分到的
            // 糖果数是其本身存储的值和当前右边小孩糖果数+1的最大值
            if(ratings[i] > ratings[i+1]) {
                result[i] = Math.max(result[i], result[i + 1] + 1);
            }
        }
        
        int sum = 0;
        for(int temp : result) sum += temp;
        return sum;
    }
}

剑指offer 面试题03 数组中重复的数字(Easy)

找出数组中重复的数字。

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

Example 1:

1
2
3

输入：
[2, 3, 1, 0, 2, 5, 3]
输出：2 或 3

限制：

1	2 <= n <= 100000

解：这道题没有说额外空间的限制，所以可以和面试官讨论一下再决定用哪种方法。

方法一：哈希表，利用哈希Set放入重复元素的时候会返回false(添加失败)来做，每次返回false的时候就将函数返回这个值即可。

class Solution {
    public int findRepeatNumber(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for(int num : nums) {
            if(!set.add(num)) {
                return num;
            }
        }
        return -1;
    }
}

时间复杂度：O(n)
空间复杂度：O(n)

方法二：抓住题目条件，所有数字范围都在0~n-1之内。如果没有重复数字，那么对每一个数排序之后其值都等于下标值。

利用这一点做哈希，遍历整个数组，如果当前数字不等于其下标，就将其和其下标位置的元素交换。在交换过程中，某个重复的数字迟早会有冲突，此时返回即可。

class Solution {
    public int findRepeatNumber(int[] nums) {
        
        for(int i = 0; i < nums.length; i++) {
            while(i != nums[i]) {
                if(nums[i] == nums[nums[i]]) {
                    return nums[i];
                }
                int temp = nums[i];
                nums[i] = nums[temp];
                nums[temp] = temp;
            }
        }
        return -1;
    }
}

时间复杂度：O(n)
空间复杂度：O(1)，空间复杂度得到了优化

146. LRU Cache(LRU缓存机制)(Mid)

Design and implement a data structure for Least Recently Used (LRU) cache. It should support the following operations: get and put.

get(key) - Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1.
put(key, value) - Set or insert the value if the key is not already present. When the cache reached its capacity, it should invalidate the least recently used item before inserting a new item.

The cache is initialized with a positive capacity.

Follow up:

Could you do both operations in O(1) time complexity?

Example:

LRUCache cache = new LRUCache( 2 /* capacity */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // returns 1
cache.put(3, 3);    // evicts key 2
cache.get(2);       // returns -1 (not found)
cache.put(4, 4);    // evicts key 1
cache.get(1);       // returns -1 (not found)
cache.get(3);       // returns 3
cache.get(4);       // returns 4

注：因为这道题在写之后会有很大的改动，所以可以记住题目原本的代码其实很短，如下：

class LRUCache {

    public LRUCache(int capacity) {
        
    }
    
    public int get(int key) {
        
    }
    
    public void put(int key, int value) {
        
    }
}

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

解：LRU cache是页面置换算法。具体使用场景：在进程运行过程中，若其所要访问的页面不在内存而需把它们调入内存，但内存已无空闲空间时，为了保证该进程能正常运行，系统必须从内存中调出一页程序或数据送磁盘的对换区中。但应将哪个页面调出，须根据一定的算法来确定。通常，把选择换出页面的算法称为页面置换算法(Page-Replacement Algorithms)。

LRU是Least Recently Used的缩写，即最近最少使用，是一种常用的页面置换算法，选择最近最久未使用的页面予以淘汰。该算法赋予每个页面一个访问字段，用来记录一个页面自上次被访问以来所经历的时间 t，当须淘汰一个页面时，选择现有页面中其 t 值最大的，即最近最少使用的页面予以淘汰。

本质上，这个替换算法和现在的推荐系统有异曲同工之妙。

推荐算法就是根据之前元素被使用的频次和被使用的时间，来预测新来的元素为某一个老元素的概率是多少。

现代计算机中，替换算法越来越使用人工智能来做了，而不是简单基于逻辑式的公式。

LRU cache源自于用得非常多的缓存的思想。它有两个比较重要的策略：大小和替换策略。除了LRU(Least Recently Used)，还有一种可以和它相似的，只是替换策略不同的缓存机制：LFU(Least Frequently Used)，具体区别可以从名字中看出。

按照题目的要求，我们自己完成的LRU cache应当保证查询与修改的时间复杂度都为O(1)。

如果最朴素的，全部自己实现，那么就是哈希表加双向链表。这样就训练一下双向链表怎么写。

所有双向链表或者单向链表的题目，没有巧，就是多练，即可。

在现实工作中，其实不太可能去手写一个链表、map、set或者排序，都是有现成的库。

有些公司可能比较刻板，需要多练一些基本功。

官方题解中，给出了两种解法，详情可以点击这里

方法一：使用有序字典这个数据结构，它综合了哈希表和链表。对于java，系统使用了LinkedHashMap这个类实现；对于Python，系统使用了OrderedDict实现字典序。

class LRUCache extends LinkedHashMap<Integer, Integer> {
    private int capacity;
    public LRUCache(int capacity) {
        super(capacity, 0.75F, true);
        this.capacity = capacity;
    }
    
    public int get(int key) {
        return super.getOrDefault(key, -1);
    }
    
    public void put(int key, int value) {
        super.put(key, value);
    }
    
    @Override
    protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
        return size() > capacity;
    }
}

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

拓展:linkedhashmap和hashmap有什么区别？
HashMap就只是一个哈希表，键值对对应，最多允许一条记录的键值为Null，而且HashMap不支持线程同步，即任一时刻如果多个线程同时写HashMap，可能导致数据的不一致性。如果需要同步，对于HashMap，可以用Collections的synchronizedMap方法使HashMap拥有同步的能力。

LinkedHashMap也是一个HashMap，但是它内部维持了一个双向链表，可以保持顺序。

总之，LinkedHashMap的内部实现原理，就是一个双向的LinkedList+HashMap,所以名字是：LinkedHashMap。

方法二：不用LinkedHashMap，自己手写双向链表+哈希表

利用哈希表，辅以双向链表记录键值对的信息，所以可以在O(1)时间内完成put和get操作，同时也支持O(1)删除第一个添加的节点。

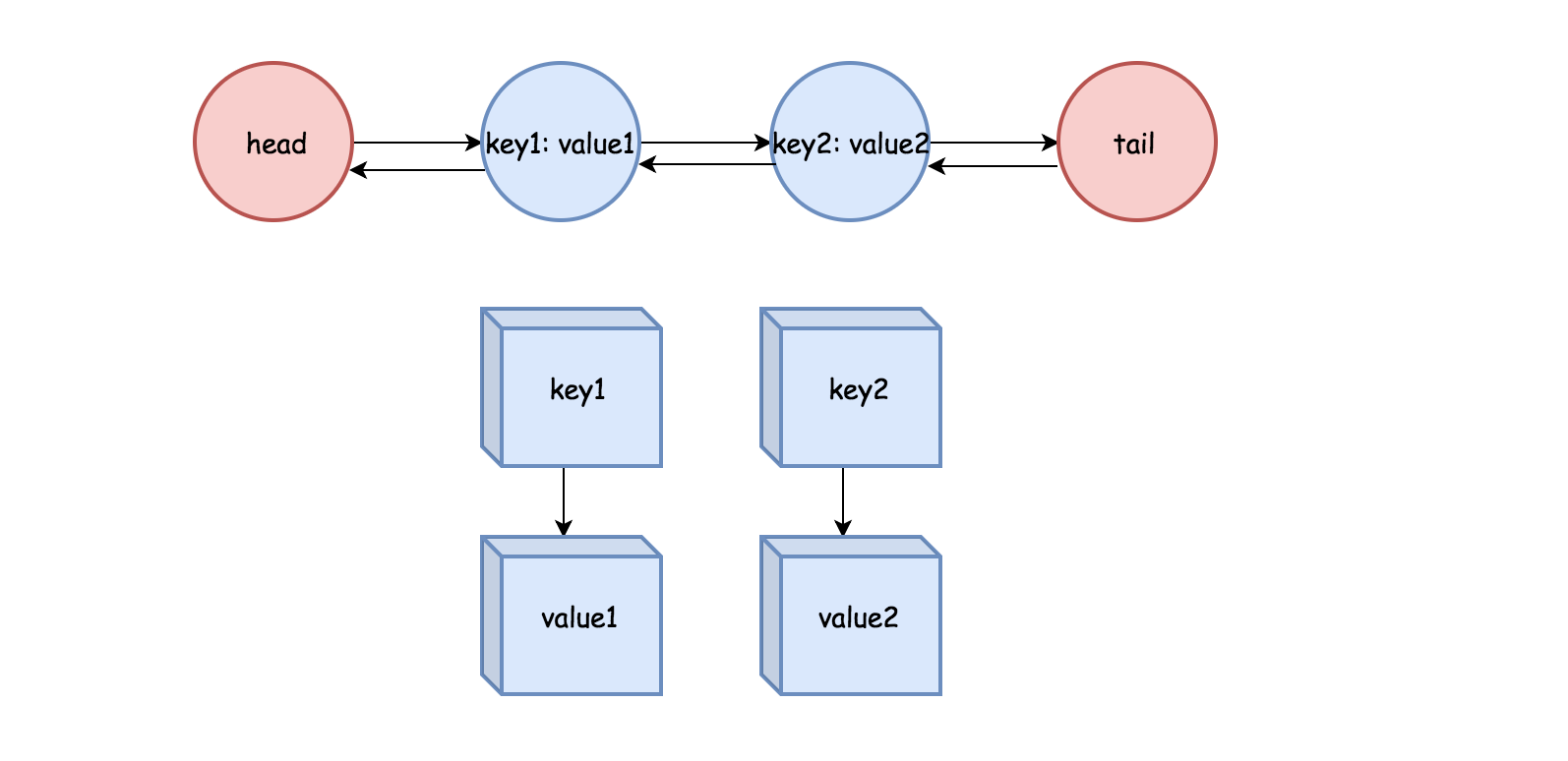
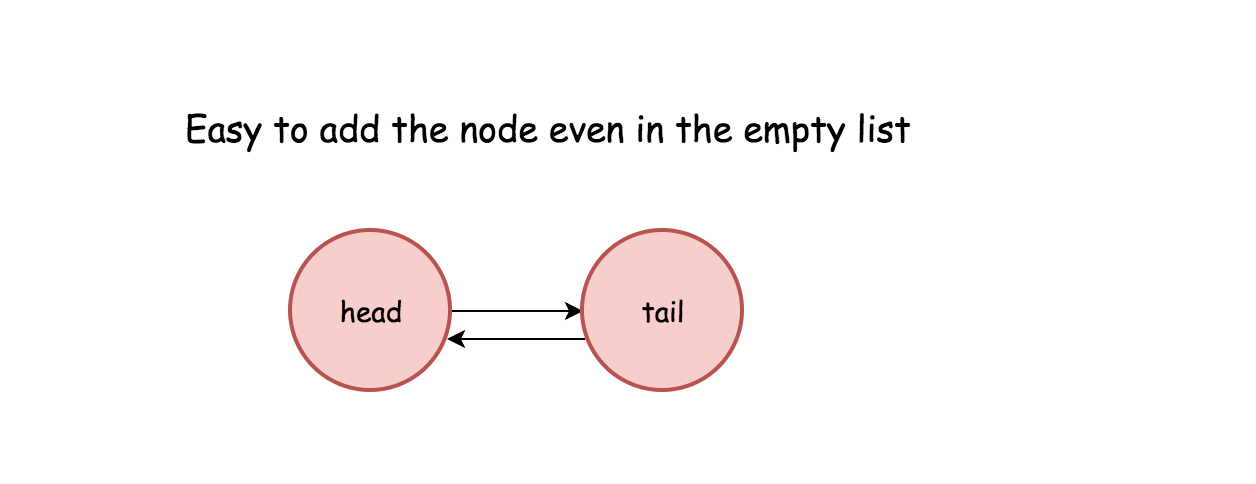
一个需要注意的是，在双向链表实现中，这里使用一个伪头部和伪尾部标记界限，这样在更新的时候就不需要检查是否是 null 节点。

至于到代码，我们需要自己定义一个双向链表的节点以及它的各种操作方法。这里定义了增加、删除、移动到头部、pop出Tail。实际上要写的只有addNode和removeNode，这两个写好了，其他两个方法只要调用它们就好。需要注意这里增加的位置是指定在head之后、删除的位置是在tail前一个。

然后需要定义缓存空间cache，完成它的三个函数：初始化、get()、put()。

这过程中我们需要两个变量：key和value，其中key就是保存某个秘钥。而value则是这个秘钥的值。(分页置换算法相关知识)

class LRUCache {
    
    class DLinkedNode {
        int key, value;
        DLinkedNode prev;
        DLinkedNode next;
    }
    
    private void addNode(DLinkedNode node) {
        // always add new node right after head
        node.next = head.next;
        node.prev = head;
        
        head.next.prev = node;
        head.next = node;
    }
    
    private void removeNode(DLinkedNode node) {
        // remove an existing node from the double LinkedList
        DLinkedNode next = node.next;
        DLinkedNode prev = node.prev;
        
        next.prev = prev;
        prev.next = next;
    }
    
    private void moveToHead(DLinkedNode node) {
        // move certain node to the head
        removeNode(node);
        addNode(node);
    }
    
    private DLinkedNode popTail() {
        // pop the current tail
        DLinkedNode target = tail.prev;
        removeNode(target);
        return target;
    }
    
    
    
    private HashMap<Integer, DLinkedNode> cache = new HashMap<>();
    private int size;
    private int capacity;
    private DLinkedNode head, tail;
    
    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        
        // 默认调用无参构造函数
        head = new DLinkedNode();
        
        tail = new DLinkedNode();
        
        head.next = tail;
        tail.prev = head;
    }
    
    public int get(int key) {
        
        DLinkedNode node = cache.get(key);
        
        if(node == null) return -1;
        
        // 成功取到，因为本身是Least Recently Used，所以最近使用的放到头部
        moveToHead(node);
        
        return node.value;
        
    }
    
    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        
        if(node == null) {
            DLinkedNode newNode = new DLinkedNode();
            newNode.key = key;
            newNode.value = value;
            
            cache.put(key, newNode);
            addNode(newNode);
            
            ++size;
            
            // 如果存不下了，要pop
            if(size > capacity) {
                // pop the tail
                DLinkedNode tail = popTail();
                cache.remove(tail.key);
                --size;
            }
        } else {
            // update the value
            node.value = value;
            moveToHead(node);
        }
    }
}

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

时间复杂度：对于put和get都是O(1)
空间复杂度：O(capacity),因为哈希表和双向链表最多存储capacity + 1个元素

寻找K数

K数是指一个数组中，它前面的数都比它小，它后面的数都比它大。找出一个数组中所有的K数

解：题目描述很简单，但是实际考虑起来需要注意，首先K数在一个数组里面很可能不止1个，然后数组的第一个的左边和数组最后一个的右边，该怎么处理？

把数组最左边设置为负无穷(Integer.MIN_VALUE),最右边设置成正无穷(Integer.MAX_VALUE),新开一个大小为原来大小+2的数组，把最左边和最右边处理完之后，依次遍历每个元素，然后以每个元素为轴，分别比较其左边和右边的每一个元素，满足左边都比它小同时右边都比它大的，这个数就是K树。

public static List<Integer> findK(int[] array) {
    int len = array.length;
    List<Integer> result = new LinkedList<>();
    // 为了存放正无穷和负无穷的数组
    int[] newArray = new int[len + 2];
    // 初始化newArray,赋值array进去，同时设置0和len-1位置
    for(int i = 1; i <= len; i++) {
        newArray[i] = array[i-1];
    }
    newArray[0] = Integer.MIN_VALUE;
    newArray[len+1] = Integer.MAX_VALUE;
    // 标记当前 i 数是否是K数，只要不满足要求就设置为false
    boolean flag = true;
    for(int i = 1; i <= len; i++) {
        // 第一次判断，i左边的所有数是否都比它小
        for(int j = 0; j <= i-1; j++) {
            if(newArray[j] >= newArray[i]) {
                flag = false;
                break;
            }
        }
        // 第二次判断，i右边的所有数是否都比它大
        if (flag) {
            for(int j = i+1; j <= len+1; j++) {
                if(newArray[j] <= newArray[i]) {
                    flag = false;
                    break;
                }
            }
        }
        // 两次判断都成功，则i就是K数
        if(flag) {
            result.add(newArray[i]);
        }
    }
    return result;
}

剑指offer21.调整数组顺序使奇数位于偶数前面(Easy)

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有奇数位于数组的前半部分，所有偶数位于数组的后半部分。

示例：

1
2
3

输入：nums = [1,2,3,4]
输出：[1,3,2,4] 
注：[3,1,2,4] 也是正确的答案之一。

提示：

1 <= nums.length <= 50000
1 <= nums[i] <= 10000

解：方法一：可以用两个指针，一头一尾，头指针先不断遍历找到偶数，然后尾指针不断遍历找到奇数，然后将两者交换即可。

class Solution {
    public int[] exchange(int[] nums) {
        
        if(nums == null || nums.length == 0) return nums;
        
        int left = 0, right = nums.length-1;
        while(left < right) {
            // 先找到左边的偶数
            while(left < right && (nums[left] & 1) != 0 ) left++;
            // 再找到右边的奇数
            while(left < right && (nums[right] & 1) == 0 ) right--;
            // 找到之后直接将两者交换。这样比写四个if-else去遍历所有情况更快
            swap(nums, left, right);
        }
        return nums;
    }
    public void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

时间复杂度：O(N),N为数组nums长度，过程下来left和right两个指针遍历整个数组。
空间复杂度：O(1)，额外开销只有两个指针

但是如果对于工程要求比较高，面试官可能更希望我们能够写出如下可以扩展的写法。怎么扩展？

我们可以把代码拆解成两部分，一部分判断数字应该在数组前半部分还是后半部分的标准；二是拆分数组的操作。

class Solution {
    public int[] exchange(int[] nums) {
        
        if(nums == null || nums.length == 0) return nums;
        
        int left = 0, right = nums.length-1;
        while(left < right) {
            // 先找到左边的偶数
            while(left < right && !isEven(nums[left]) ) left++;
            // 再找到右边的奇数
            while(left < right && isEven(nums[right]) ) right--;
            // 找到之后直接将两者交换。这样比写四个if-else去遍历所有情况更快
            swap(nums, left, right);
        }
        return nums;
    }
    public void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    
    public boolean isEven(int n) {
        return (n&1) == 0;
    }
}

方法二：也是用两个指针，但是一快一慢。快的在前，找到奇数就和慢指针指向的元素交换。

操作流程：

定义快慢双指针 fast 和 low ，fast 在前， low 在后 .
fast 的作用是向前搜索奇数位置，low 的作用是指向下一个奇数应当存放的位置
fast 向前移动，当它搜索到奇数时，将它和 nums[low] 交换，此时 low 向前移动一个位置 .
重复上述操作，直到 fast 指向数组末尾 .

class Solution {
    public int[] exchange(int[] nums) {
        if(nums == null || nums.length == 0) return nums;
        int slow = 0, fast = 0;
        while(fast < nums.length) {
            if((nums[fast] & 1) != 0) {
                swap(nums, slow, fast);
                slow++;
            }
            fast++;
        }
        return nums;
    }
    public void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

13. Roman to Integer(罗马数字转整数)(Easy)

Roman numerals are represented by seven different symbols: I, V, X, L, C, D and M.

Symbol       Value
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

For example, two is written as II in Roman numeral, just two one’s added together. Twelve is written as, XII, which is simply X + II. The number twenty seven is written as XXVII, which is XX + V + II.

Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not IIII. Instead, the number four is written as IV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as IX. There are six instances where subtraction is used:

I can be placed before V (5) and X (10) to make 4 and 9.
X can be placed before L (50) and C (100) to make 40 and 90.
C can be placed before D (500) and M (1000) to make 400 and 900.

Given a roman numeral, convert it to an integer. Input is guaranteed to be within the range from 1 to 3999.

Example 1:

1 2	Input: "III" Output: 3

Example 2:

1 2	Input: "IV" Output: 4

Example 3:

1 2	Input: "IX" Output: 9

Example 4:

1
2
3

Input: "LVIII"
Output: 58
Explanation: L = 50, V= 5, III = 3.

Example 5:

1
2
3

Input: "MCMXCIV"
Output: 1994
Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.

解：实际上就是类似map的对应的关系，但是这里不用Map，用switch，能够快很多：

import java.util.*;

class Solution {
    public int romanToInt(String s) {
        int sum = 0;
        int preNum = getValue(s.charAt(0));
        for(int i = 1;i < s.length(); i ++) {
            int num = getValue(s.charAt(i));
            if(preNum < num) {
                sum -= preNum;
            } else {
                sum += preNum;
            }
            preNum = num;
        }
        sum += preNum;
        return sum;
    }
    
    private int getValue(char ch) {
        switch(ch) {
            case 'I': return 1;
            case 'V': return 5;
            case 'X': return 10;
            case 'L': return 50;
            case 'C': return 100;
            case 'D': return 500;
            case 'M': return 1000;
            default: return 0;
        }
    }
}