LeetCode Dynamic Programming

每个人都是自己命运的主宰——斯蒂尔斯

LeetCode大量动态规划相关题目，其解决思路和具体代码。

动态规划不是空中楼阁。

dynamic programming最常用的场景就是当你的结果存在大量重复的过程的时候，可以用DP利用你在过程中得到的结果。

70. Climbing-stairsl(爬楼梯)(Easy)

You are climbing a stair case. It takes n steps to reach to the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Note: Given n will be a positive integer.

Example 1:

Input: 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:

Input: 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

---

解：爬楼梯很经典，变型也很多。首先结论是，单纯的这道题，通过数学归纳的思路(或者说递归的思路)，不难发现其实结果就是前两个元素为1,2的斐波那契数列。(斐波那契数列为509题，因为类似这里就不记录了，链接点击这里)

方法一：递归，可以画出递归树发现，因为每个层级都会在上一层的数量基础上多出2倍的节点，所以时间复杂度为O(2^n)，指数级别，不可以接受。而且实际测试中在N为44的时候会出现超时。

class Solution {
    public int climbStairs(int n) {
        if(n <= 2) return n;
        return climbHelper(0,n);
    }
    
    public int climbHelper(int curr, int target) {
        // terminator
        // 跨过了目标阶梯，不算入方法
        if(curr > target) return 0;
        
        // 刚好攀登到某个位置
        if(curr == target) return 1;
        
        return climbHelper(curr + 1, target) + climbHelper(curr + 2, target);
    }
}

方法二：基于递归，加上备忘录，进行有记忆的递归，可以把之前计算过的结果保存下来，有很好的剪枝效果。因为有记录所有的过程，所以子问题的数量就是f(1),f(2)…，为O(n),而且每个子问题解决的时间为O(n)

class Solution {
    public int climbStairs(int n) {
        // 基于暴力递归，进行有记忆的递归，把每一步的结果存储在mem数组之中，每当有函数被再次调用，就直接从memo数组返回结果，减少计算次数
        int[] memo = new int[n+1];
        if(n <= 2) return n;
        return climbHelper(0,n,memo);
    }
    
    public int climbHelper(int curr, int target, int[] memo) {
        // terminator
        // 跨过了目标阶梯，不算入方法
        if(curr > target) return 0;
        
        // 刚好攀登到某个位置
        if(curr == target) return 1;
        
        // 如果当前N阶梯数量已经计算过，直接从memo返回
        if(memo[curr] > 0) return memo[curr];
        
        memo[curr] =  climbHelper(curr + 1, target, memo) + climbHelper(curr + 2, target, memo);
        return memo[curr];
    }
}

方法三：常规动态规划，时间复杂度为O(n)，空间复杂度也为O(n)

class Solution {
    public int climbStairs(int n) {
        if(n <= 2) return n;
        
        // dp[i]表示爬到第i阶共有的爬法
        int[] dp = new int[n+1];
        dp[1] = 1; dp[2] = 2;
        for(int i = 3; i <= n; i++) {
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
}

方法四：基于常规动态规划的优化。在空间复杂度上可以提升到O(1)。实际上在一开始的时间复杂度的基础上都可以进行空间的优化，比如O(n)可以优化到O(1),O(m*n)可以优化到O(n)。

class Solution {
    public int climbStairs(int n) {
        if(n <= 2) return n;
        
        int f1 = 1, f2 = 2, f3 = 0;
        for(int i = 3; i <= n; i++) {
            f3 = f1 + f2;
            f1 = f2;
            f2 = f3;
        }
        return f3;
    }
}

322. Coin Change(零钱兑换)(Mid)

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

Example 1:

Input: coins = [1, 2, 5], amount = 11
Output: 3 
Explanation: 11 = 5 + 5 + 1

Example 2:

Input: coins = [2], amount = 3
Output: -1

Note:

You may assume that you have an infinite number of each kind of coin.

---

解：这道题其实和之前的爬楼梯问题是异曲同工之处，可以看成每次可以走coins数组里面的步伐，最后要到达amount的高度，有多少种走法。当然这里有点变化，就是比如112和121，在爬楼梯问题是不同方法，而在这里coin change则是相同的，一种方法。但是写DP方程的话差不多了。

方法一：暴力法，用递归的方式。

题目变成：在状态树中找到叶子节点为0的，并且层数最小的。
可以用树的广度优先遍历，直到碰到数值为0的节点，当前层数就是最小硬币数，就是我们的答案。

但是这个方法会存在指数级别的时间复杂度。

方法二：DP

a. subproblems

b. DP array：f(n) = min{f(n-k), for k in [1,2,5]} + 1, 遍历可以选择的面值的数组，直到n被减到0为止，然后取得到的硬币数的最小值。加一是因为一开始的n-k没有被算入，后面补上。

c. DP方程

代码：

class Solution {
    public int coinChange(int[] coins, int amount) {
        // amount + 1 是无法到达的，以此判断最后是否不能到达amount
        int max = amount+1;
        // dp数组的下标是当前金额，里面的值是需要的硬币的个数，初始化是不可达的max
        int[] dp = new int[max];
        // 初始化dp,初始化考虑只有面值为1的硬币，需要max个
        Arrays.fill(dp,max);
        // 当拿到的amount是0的时候，需要0个硬币，类似爬楼梯，初始化就在0级台阶
        dp[0] = 0;
        // 外层，遍历所有下标的元素，也就是当前凑到的面值数
        for(int i = 1; i <= amount; i++) {
            // 每次都从coins里面取元素出来，比如coins是[1,2,5]，每次在要凑下标
            // 值的时候，都会把1,2,5取出来进行值的拼凑
            for(int j = 0; j < coins.length; j++) {
                // 如果当前coins里面取出来的值比下标小，才能用。否则比如你下标是3，
                // 即当前要凑到3的值，但当前conis里面硬币值是10，那肯定不用这个
                if(coins[j] <= i) {
                    // 用DP方程进行递推
                    dp[i] = Math.min(dp[i], dp[i-coins[j]] + 1);
                }
            }
        }
        // 如果最后一个没有被修改，则没办法组成这个金额。否则返回最后amount下标的值
        return dp[amount] == max ? -1 : dp[amount];
    }
}

动态规划一般脱离递归，直接由循环迭代完成计算。

动态规划问题最难的就是写出状态转移方程。

时间复杂度：O(m*n)

343. Integer Break(整数拆分)(Mid)

Given a positive integer n, break it into the sum of at least two positive integers and maximize the product of those integers. Return the maximum product you can get.

Example 1:

Input: 2
Output: 1
Explanation: 2 = 1 + 1, 1 × 1 = 1.

Example 2:

Input: 10
Output: 36
Explanation: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36.

Note:You may assume that n is not less than 2 and not larger than 58

注：这道题和剑指offer上第14，剪绳子，题目不同，但是考察内容非常类似。链接可以点击这里

---

解：这道题可以用纯数学思路和动态规划两种方法解决

方法一：纯数学，其实就是通过分析之后用贪心法。可以用数学归纳法证明，目标是拆分成多个3的乘积，并且能拆分成2*2就不拆分成 1 * 3。

详细内容可以参考这篇题解

简而言之，要尽可能把数字拆分成3或者3的倍数。但是按照题目要求，至少要剪一次，至少要两段，所以边界条件值(n小于等于3的时候)可以考虑返回n-1.

因为拆分成2比拆分成3乘积更小，所以3优先级大于2,2大于1

然后要求出n除以3的整数部分a和余数部分b(即n=3*a+b)，要分成三种情况：

1. 当b=0时，直接返回3^a;
2. 当b=1时，要将一个1+3转换成2+2，因为2*2 > 1 * 3，因此返回 3^(a-1) * 4;
3. 当b=2时，返回3^n*2即可

代码如下：

class Solution {
    public int integerBreak(int n) {
        if(n <= 3) return n-1;
        int a = n / 3, b = n % 3;
        if(b == 0) return (int)Math.pow(3,a);
        if(b == 1) return (int)Math.pow(3, a-1) * 4;
        return (int)Math.pow(3,a) * 2;
    }
}

• 时间复杂度为O(1)，仅有求整、取余、次方计算操作
• 空间复杂度：O(1)，只需要变量a和b和常数大小的额外空间

221. Maximal Square(最大正方形)(Mid)

Given a 2D binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.

Example:

Input: 

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

Output: 4

---

解：别误读了题意，输入只是二维matrix，要找Square而已！

这道题看上去和”Stack-Queue”系列的84、85题好像很类似，但是做法和思路完全不同，而且也比那两道题更简单……主要的原因是正方形比矩形性质好用太多，直接用动态规划的思想即可。

发现规律：申请一个dp[][][]二维数组，通过找规律和观察，可以发现，如果某个位置的值为1，那么这个位置上的值取决于它的上面、左上角、左边三个值的最小值加1.

然后每次都检查当前存储的值是否可以替换掉之前的maxSquare值即可。

因为最后求的是area，所以直接返回maxSquare*maxSquare即可。

class Solution {
    public int maximalSquare(char[][] matrix) {
        if(matrix == null || matrix.length == 0) return 0;
        // 注意rows和cols的值，别弄反了
        int rows = matrix.length, cols = matrix[0].length;
        // 最大边长
        int maxSquare = 0;
        // 申请dp数组，大小比行和列都多1，这样可以防止处理的时候越界
        // 申请的时候多申请1，这道题可以不用考虑边界情况，直接把
        // 原本的数组重新"填"到dp数组里，值是当前能组成的最大Square
        int[][] dp = new int[rows + 1][cols + 1];
        for(int i = 1; i <= rows; i++) {
            for(int j = 1; j <= cols; j++) {
                if(matrix[i - 1][j - 1] == '1') {
                    // 取当前左、上、左上三个方向的最小值，再加1
                    // Math.min函数一次最多只能有两个参数，要注意
                    dp[i][j] = Math.min(dp[i - 1][j - 1],Math.min(dp[i][j - 1],dp[i - 1][j])) + 1;
                    maxSquare = Math.max(maxSquare, dp[i][j]);
                }
            }
        }
        return maxSquare * maxSquare;
    }
}

303.Range Sum Query-Immutable(区域和检索-数组不可变)(Easy)

Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.

Example:

Given nums = [-2, 0, 3, -5, 2, -1]

sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3

Note:

1. You may assume that the array does not change.
2. There are many calls to sumRange function.

---

解：动态规划的思路解决，预先将所有的相加可能的结果计算出来并存储起来，然后调用它来找到即可。注意下标问题。

class NumArray {
    int sums[];
    public NumArray(int[] nums) {
        sums = new int[nums.length + 1];
        sums[0] = 0;
        for(int i = 0;i < nums.length; i++) {
            sums[i+1]  = sums[i] + nums[i];
        }
    }
    public int sumRange(int i, int j) {
        return sums[j+1] - sums[i];
    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * int param_1 = obj.sumRange(i,j);
 */

注意，先把所有计算结果保存起来，每次访问的话只需要O(1)，否则每次访问再计算，会导致时间复杂度太高。

53.Maximum Subarray(最大子序和)

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Follow up:

If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

---

解：动态规划，定义数组dp[n.length]，其中dp[i]表示当前第i个元素可以得到的最大和，递推公式关键在于dp[i]为nums[i]与dp[i-1]+nums[i]之间的最大值，因为每次两种选择，直接加入nums[i]，或者从之前dp[i]和都小于0，需要重新从nums[i]开始算起。而在过程中需要记录当前能得到的最大的子序和max，最后返回max即可。

为什么要有一个max记录最大值？状态都放在dp[i]不就行了？——不可以，答案很可能是子序和，所以要有一个单独的变量保存结果。

class Solution {
    public int maxSubArray(int[] nums) {
        int len = nums.length;
        // dp[i]表示第i位置到上一个计算起点的最大子序和的值
        int[] dp = new int[len];
        int result = nums[0];
        dp[0] = nums[0];
        for(int i = 1; i < len; i++) {
            // 比较巧妙，如果dp[i-1]<0，那么肯定丢弃dp[i-1]能让dp[i]更大
            // 反之同理，如果dp[i-1] > 0，那么加上dp[i-1]能让dp[i]更大
            dp[i] = nums[i] + (dp[i-1] > 0 ? dp[i-1] : 0);
            result = Math.max(dp[i], result);
        }
        return result;
    }
}

300.Longest Increasing Subsequence(最长上升子序列)

Given an unsorted array of integers, find the length of longest increasing subsequence.

Example:

Input: [10,9,2,5,3,7,101,18]
Output: 4 
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

Note:

• There may be more than one LIS combination, it is only necessary for you to return the length.
• Your algorithm should run in O(n^ 2) complexity.

Follow up: Could you improve it to O(n log n) time complexity?

---

解：这道题非常重要，如果面试中出现了，现场想基本是想不到的。

方法一：暴力，时间是指数级别O(2^n)，因为要以每个数为中心，然后右边只要碰到比它大的就要继续往后探索。比如当前为2，碰到5要继续让5往后分叉，到7,7还要继续往后，等等。

方法二：动态规划，记录dp[i]的结果，自底向上思考，定义dp[i]为以当前第i位数字为结尾能够组成的LIS，则最后返回的结果是max(k=1,2...n)dp[k]。

一开始我们把dp数组所有元素填上1，因为每个元素一定能用自己组成一个结果。

class Solution {
    public int lengthOfLIS(int[] nums) {
        // base case
        if(nums.length <= 1) {
            return nums.length;
        }
        int[] dp = new int[nums.length];
        Arrays.fill(dp,1);
        
        int result = 1;
        
        for(int i = 1; i < nums.length; i++) {
            for(int j = 0; j < i ;j++) {
                if(nums[i] > nums[j]) {
                    //dp[i]每次的选择有两个：用dp[j]或者不用。
                    //如果用dp[j]里面的值，则在dp[j]基础上加1
                    //如果不用，说明用nums[i]组成的子序列更长，直接用dp[i]即可
                    dp[i] = Math.max(dp[i], dp[j]+1);
                }
                //每次以i为轴，记录每轮最大的结果，保存到result中
                result = Math.max(result,dp[i]);
            }
        }
        return result; 
    }
}

时间复杂度：O(n^2)

空间复杂度：O(n)

但是实际上，单纯用动态规划的时间复杂度太高了，面试的时候面试官不会满意的。

方法三：最优解，用binary search，二分查找来解决，时间复杂度可以到O(NlogN)

之前用dp的时候是自底向上的思路，那么如果我们正向来思考呢？

我们从左往右遍历，自己构建出来这个目标结果数组。每遍历到一个数，我们就判断这个数应该在我们最长上升子序列的哪个部分，然后更新这个部分。每次构造的数字实际上只能有三种情况：放到结果数组的第一位、插入到第中间、放到最后——只有放在最后，长度才+1。而如果放在中间，则只有新来的数比之前中间的小，才能让整体上升序列更长。

所以总结来说，可以观察到，如果出现新的最大值，整个数组长度会+1，如果遇到新的最大值比当前最大值小，那么就会更新dp的最大值因为后面出现的最大值一定可以被加到之前的连续上升subsequence当中，因为最后一个元素能更小的话这个边界肯定是最优的。所以这样我们最后得到的dp数据可能不对，但是长度肯定没错。

具体解法：

首先我们可以用Java的Arrays类中的binarySearch()方法进行二分搜索。该方法返回要搜索元素的索引值。

介绍一下binarySearch()方法：

binarySearch(Object[] a,int fromIndex, int toIndex, Object key)

a:要搜索的数组

fromIndex：指定范围的开始处索引(包含)

toIndex：指定范围的结束处索引(不包含)

key：要搜索的值

Note:Arrays.binarySearch() method returns index of the search key, if it is contained in the array, else it returns (-(insertion point) - 1). The insertion point is the point at which the key would be inserted into the array; the index of the first element greater than the key, or a.length if all elements in the array are less than the specified key.

如果要搜索的元素key在指定的范围内，则返回搜索值的索引；否则返回-1或“-“(插入点)，所谓插入点的值就是第一个比关键字大的元素在数组中的位置索引，而且这个位置索引从1开始，或者如果整个数组所有元素都比这个key小，那么返回的是-(a.length+1)。返回-1的情况是一开始查找的数组中也没有元素(即数组长度为0)的边界情况。

有关binarySearch()的介绍可以参考这篇文章

这道题解法讲解可以参考这个视频

注意这个函数是被重载的，在这里只介绍这种参数形式。

用binarySearch()优化之后的dp方法：

public class Solution {
    public int lengthOfLIS(int[] nums) {            
        int[] dp = new int[nums.length];
        int len = 0;

        for(int num : nums) {
            //范围是0~len，每次查找的元素是x
            int index = Arrays.binarySearch(dp, 0, len, num);
            if(index < 0) { //没有重复元素。之后会直接返回插入点，若没找到，
                //插入点是从1开始最后又加上负号的值，所以i要先加1再取负才是新元素应该在
                //dp数组中的具体位置
                index = -(index + 1);//一开始插入的时候，实际坐标其实是-(-1+1)=0
            }
            // 找到插入点后将元素x插入递增数组dp对应位置
            dp[index] = num;
            if(index == len) //若插入的位置在最后，len++，这也是唯一会让len增加的情况
                len++;
        }

        return len;
    }
}

• 时间复杂度：O(NlogN)
• 空间复杂度：O(n)

但是如果面试中面试官不允许使用Arrays.binarySearch，则可以我们自己手写一个二分查找的代码：

class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] tails = new int[nums.length];
        int len = 0;
        for(int num : nums) {
            int left = 0, right = len;
            //手写二分查找算法，找到插入的位置left
            while(left != right) {
                int mid = (left + right) >> 1;
                if(tails[mid] < num)
                    left = mid + 1;
                else 
                    right = mid;
            }
            tails[left] = num;
            if(left == len) 
                len++;
        }
        return len;
    }
}

剑指offer 62.圆圈中最后剩下的数字(Easy)

0,1,,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。

例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

示例 1：

输入: n = 5, m = 3
输出: 3

示例 2：

输入: n = 10, m = 17
输出: 2

限制：

• 1 <= n <= 10^5
• 1 <= m <= 10^6

---

解：方法一：用双向链表(或者用单向链表模拟双向链表)来删除。

class Solution {
    public int lastRemaining(int n, int m) {
        // idx为每次删除元素的位置
        ArrayList<Integer> list = new ArrayList<>(n);
        for(int i = 0; i < n; i++) {
            list.add(i);
        }
        int idx = 0;
        // n为环中剩余的元素数量而不是下标，所以n最后要为1
        while(n > 1) {
            // idx为当前要删除的元素的下标
            idx = (idx + m - 1) % n;
            list.remove(idx);
            n--;
        }
        return list.get(0);
    }
}

• 时间复杂度：因为看到ArrayList中的源码，删除操作需要遍历一遍链表，所以整个时间复杂度趋近于O(mn)或O(n^2)
• 空间复杂度：O(n)

方法二：这是非常经典的约瑟夫环问题，考虑最后剩余的1个圆环的位置，发现有规律！直接用数学方法解决，通过每轮删除元素的下标的值，如果从0开始倒着推，可以找到如下规律：

第一轮是 [0, 1, 2, 3, 4] ，所以是 [0, 1, 2, 3, 4] 这个数组的多个复制。这一轮 2 删除了。

第二轮开始时，从 3 开始，所以是 [3, 4, 0, 1] 这个数组的多个复制。这一轮 0 删除了。

第三轮开始时，从 1 开始，所以是 [1, 3, 4] 这个数组的多个复制。这一轮 4 删除了。

第四轮开始时，还是从 1 开始，所以是 [1, 3] 这个数组的多个复制。这一轮 1 删除了。

最后剩下的数字是 3。

图中的绿色的线指的是新的一轮的开头是怎么指定的，每次都是固定地向前移位 mm 个位置。

然后我们从最后剩下的 3 倒着看，我们可以反向推出这个数字在之前每个轮次的位置。

最后剩下的 3 的下标是 0。

第四轮反推，补上 m 个位置，然后模上当时的数组大小 2，位置是(0 + 3) % 2 = 1。

第三轮反推，补上 m 个位置，然后模上当时的数组大小 3，位置是(1 + 3) % 3 = 1。

第二轮反推，补上 m 个位置，然后模上当时的数组大小 4，位置是(1 + 3) % 4 = 0。

第一轮反推，补上 m 个位置，然后模上当时的数组大小 5，位置是(0 + 3) % 5 = 3。

所以最终剩下的数字的下标就是3。因为数组是从0开始的，所以最终的答案就是3。

总结一下反推的过程，就是 (当前index + m) % 上一轮剩余数字的个数。

所以公式为：最终被删元素下标 = (当前index + m) % 上一轮剩余数字的个数

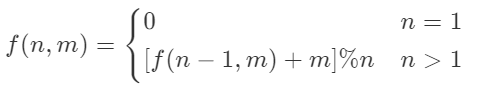
用代码来写就比较容易了：

class Solution {
    public int lastRemaining(int n, int m) {
        if(n < 1 || m < 1) return -1;
        int result = 0;
        //最后一轮剩两个人，从2开始反推
        for(int i = 2; i <= n; i++) {
            result = (result + m) % i;
        }
        return result;
    }
}

• 时间复杂度：O(n)
• 空间复杂度：O(1)

无理论是时间复杂度还是空间复杂度都优于用环形链表模拟圆环的经典解法(后者时间复杂度O(mn)、空间复杂度O(n))。有关约瑟夫环递推公式推理可以参考LeetCode题解，重点是自底向上地反推。

剑指offer 63/LC121.股票的最大利润(Mid)

Say you have an array for which the ith element is the price of a given stock on day i.

If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Note that you cannot sell a stock before you buy one.

Example 1:

Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
             Not 7-1 = 6, as selling price needs to be larger than buying price.

Example 2:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

---

解：这道题可以牵扯出买卖股票的一系列问题(121,122,123,188,309,714)，这里暂时只介绍121这道最基础的情况。

由于不用考虑交易的次数和交易冷冻时期，所以这道题场景比较简单，只需要定义一个二维数组即可，大小为dp [len] [2]，其中第二位只可能有两种情况，0或1,0代表当前没有股友股票，1代表当前持有股票。

需要注意考虑边界情况，即第一天如果没有股票，则收益为0；如果有股票，则可以看做是新买入。

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0) return 0;
        int len = prices.length;
        //dp[][]表示第i天是否持有股票时候的利润
        int[][] dp = new int[len][2];
        //第1天不持有股票，利润是0
        dp[0][0] = 0;
        //第1天就持有股票，必须买入，故此时利润是-prices[0]
        dp[0][1] = -prices[0];
        for(int i = 1; i < len; i++) {
            //第i天买入股票或卖出股票
            //0代表不持有，有两种：
            //第i天不买入也不卖出，或者卖出。
            //前者利润和i-1天不持有股票一样
            //后者利润是i-1天持有股票的利润加上股票的价值
            dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
            //1为第i天持有股票时候的利润，也是两种情况：
            //一个是第i-1天拥有股票，那么这一天的收益和前一天拥有股票时收益相同
            //一个是第i-1天没有股票，则要新买入，收益是"-股票价格"
            dp[i][1] = Math.max(-prices[i], dp[i-1][1]);
        }
        //最大利润的情况一定是最后一天不持有股票的时候的盈利值
        return dp[len-1][0];
    }
}