0%

LeetCode Stack, Queue

Posted on Edited on In
Symbols count in article: 25k

衡量一个人真正的品德，是看他在知道没有人看见的时候做些什么 —— 孟德斯鸠

分析讨论栈、队列、优先队列、双端队列以及相关LeetCode题目。

java中，队列Queue是一种特殊的线性表，实例化的时候用链表(new LinkedList<>())、栈Stack有单独的类，实例化的时候使用Stack(new Stack<>())。 队列因为用LinkedList实现,一般操作size()方法。而栈可以使用empty()或者isEmpty()判空(empty()和isEmpty()没有本质区别，一般可以通用)

事实上，普通的栈和队列在工作中基本不会使用，而用得比较多的是双端队列。比如本文中曾经在239题中使用了java库中的双端队列，并用Array实现：Deque<Integer> dq = new ArrayDeque<>();

20.Valid Parentheses(有效的括号)(Easy)

Given a string containing just the characters '(', ')', '{', '}', '[' and']', determine if the input string is valid.

An input string is valid if:

  1. Open brackets must be closed by the same type of brackets.
  2. Open brackets must be closed in the correct order.

Note that an empty string is also considered valid.

Example 1:

1
2
Input: "()"
Output: true

Example 2:

1
2
Input: "()[]{}"
Output: true

Example 3:

1
2
Input: "(]"
Output: false

Example 4:

1
2
Input: "([)]"
Output: false

Example 5:

1
2
Input: "{[]}"
Output: true

解：想要符合闭合的括号的标准，用一个栈保存和左括号对应的右括号。每次碰到左括号就入栈对应的右括号，碰到右括号就判断是否和当前栈顶元素相同。

注意有两个判空，一个是碰到右括号，如果此时栈为空，那么不能pop()(会报错)，如果此时栈为空则不为有效括号。另一个情况是所有括号都遍历完了，此时如果栈不为空，则不是有效括号。所以在遍历完s之后需要返回stack.isEmpty()。

需要注意最后一个判断因为有pop()操作，所以必须把pop()放在后面才行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack = new Stack<>();
        for(char c : s.toCharArray()) {
            if(c == '(') {
                stack.push(')');
            } else if(c == '[') {
                stack.push(']');
            } else if(c == '{') {
                stack.push('}');
            } else if(stack.isEmpty() || stack.pop() != c) {
                return false;
            }    
        }
        return stack.isEmpty();
    }
}

155.Min Stack(最小栈)(Easy)

Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.

  • push(x) – Push element x onto stack.
  • pop() – Removes the element on top of the stack.
  • top() – Get the top element.
  • getMin() – Retrieve the minimum element in the stack.

Example:

1
2
3
4
5
6
7
8
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> Returns -3.
minStack.pop();
minStack.top();      --> Returns 0.
minStack.getMin();   --> Returns -2.

解：java语言本身已经定义好了一种传统作用的Stack，这道题有什么意义呢？事实上这道题就是要实现一个可以获得最小元素的栈。

换个角度看，要能够在常数时间内检索到最小元素的栈，是不是有点像优先队列？——其实不一样，它还是一个先入后出的栈。它只是能让你在常规时间中探索到最小元素，而不是取的时候每次都取最小元素。它的api本身和栈一模一样，只是多了一个功能，能够探测到最小元素。

给出两种方法，分别用两个栈和一个栈实现。

解法一：用两个栈实现，一个数据栈，一个辅助栈。这种写法注意了健壮性，考虑了栈为空的情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class MinStack {

    // 数据栈和辅助栈同步,后面每个操作两个栈都进行相同操作
    Stack<Integer> data;
    Stack<Integer> helper;
    
    /** initialize your data structure here. */
    public MinStack() {
        // 初始化两个栈
        data = new Stack<Integer>();
        helper = new Stack<Integer>();
    }
    
    public void push(int x) {
        data.push(x);
        if(helper.isEmpty() || helper.peek() >= x) {
            helper.push(x);
        } else {
            helper.push(helper.peek());
        }
    }
    
    public void pop() {
        if(!data.isEmpty()) {
            data.pop();
            helper.pop();
        }
    }
    
    public int top() {
        if(!data.isEmpty()) {
            return data.peek();
        }
        throw new RuntimeException("栈中元素为空，此操作非法");
    }
    
    public int getMin() {
        if(!helper.isEmpty()) {
            return helper.peek();
        }
        throw new RuntimeException("栈中元素为空，此操作非法");
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

解法二：用一个栈解决。解法一开辟了一个helper栈去保存最小值，实际上我们可以用一个变量,min,去保存这个最小值。
这里有两个问题：

  1. min保存了当前的最小值，如果min更新了，那么如何保存之前的最小值呢？——把之前的min在新元素之前入栈，也就是说来了新的更小的元素，旧的最小的元素需要再次入栈以求保存。
  2. 如果当前出栈的是最小值，我们在出栈当前元素之余，还需要再出栈一次，并且把这一次出栈的值赋给min。因为最小的元素入栈前会把之前最小的元素入栈，所以这样做就把旧的最小元素保存下来了。

详细题解：点击这里

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class MinStack {

    int min = Integer.MAX_VALUE;
    Stack<Integer> stack;
    
    /** initialize your data structure here. */
    public MinStack() {
        stack = new Stack<>();
    }
    
    public void push(int x) {
        // only push the old minimum value when the current
        // minimum value changes after pushing the new value x
        if(x <= min) {
            stack.push(min);
            min = x;
        }
        stack.push(x);
    }
    
    public void pop() {
        // if pop operation could result in the changing of the current minimum value,
        // pop twice and change the current minimum value to the last minimum value
        if(stack.pop() == min) min = stack.pop();
    }
    
    public int top() {
        return stack.peek();
    }
    
    public int getMin() {
        return min;
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

641.Design Circular Deque(设计循环双端队列)(Mid)

Design your implementation of the circular double-ended queue (deque).

Your implementation should support following operations:

  • MyCircularDeque(k): Constructor, set the size of the deque to be k.
  • insertFront(): Adds an item at the front of Deque. Return true if the operation is successful.
  • insertLast(): Adds an item at the rear of Deque. Return true if the operation is successful.
  • deleteFront(): Deletes an item from the front of Deque. Return true if the operation is successful.
  • deleteLast(): Deletes an item from the rear of Deque. Return true if the operation is successful.
  • getFront(): Gets the front item from the Deque. If the deque is empty, return -1.
  • getRear(): Gets the last item from Deque. If the deque is empty, return -1.
  • isEmpty(): Checks whether Deque is empty or not.
  • isFull(): Checks whether Deque is full or not.

Example:

1
2
3
4
5
6
7
8
9
10
MyCircularDeque circularDeque = new MycircularDeque(3); // set the size to be 3
circularDeque.insertLast(1);			// return true
circularDeque.insertLast(2);			// return true
circularDeque.insertFront(3);			// return true
circularDeque.insertFront(4);			// return false, the queue is full
circularDeque.getRear();  			// return 2
circularDeque.isFull();				// return true
circularDeque.deleteLast();			// return true
circularDeque.insertFront(4);			// return true
circularDeque.getFront();			// return 4

Note:

  • All values will be in the range of [0, 1000].
  • The number of operations will be in the range of [1, 1000].
  • Please do not use the built-in Deque library.

解：使用链表完成这个API的设计。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
class MyCircularDeque {

    class DoubleListNode {
        DoubleListNode pre;
        DoubleListNode next;
        int val;
        public DoubleListNode(int val) {
            this.val = val;
        }
    }
    
    int size;
    int k;
    DoubleListNode head;
    DoubleListNode tail;
    
    /** Initialize your data structure here. Set the size of the deque to be k. */
    public MyCircularDeque(int k) {
        head = new DoubleListNode(-1);
        tail = new DoubleListNode(-1);
        head.pre = tail;
        tail.next = head;
        this.k = k;
        this.size = 0;
    }
    
    /** Adds an item at the front of Deque. Return true if the operation is successful. */
    public boolean insertFront(int value) {
        if(size == k) return false;
        DoubleListNode node = new DoubleListNode(value);
        node.next = head;
        node.pre = head.pre;
        head.pre.next = node;
        head.pre = node;
        size++;
        return true;
    }
    
    /** Adds an item at the rear of Deque. Return true if the operation is successful. */
    public boolean insertLast(int value) {
        if (size == k) return false;
        DoubleListNode node = new DoubleListNode(value);
        node.next = tail.next;
        tail.next.pre = node;
        tail.next = node;
        node.pre = tail;
        size++;
        return true;
    }
    
    /** Deletes an item from the front of Deque. Return true if the operation is successful. */
    public boolean deleteFront() {
        if (size == 0) return false;
        head.pre.pre.next = head;
        head.pre = head.pre.pre;
        size--;
            return true;
    }
    
    /** Deletes an item from the rear of Deque. Return true if the operation is successful. */
    public boolean deleteLast() {
        if (size == 0) return false;
        tail.next.next.pre = tail;
        tail.next = tail.next.next;
        size--;
            return true;
    }
    
    /** Get the front item from the deque. */
    public int getFront() {
        return head.pre.val;
    }
    
    /** Get the last item from the deque. */
    public int getRear() {
        return tail.next.val;
    }
    
    /** Checks whether the circular deque is empty or not. */
    public boolean isEmpty() {
        return size == 0;
    }
    
    /** Checks whether the circular deque is full or not. */
    public boolean isFull() {
        return size == k;
    }
}

/**
 * Your MyCircularDeque object will be instantiated and called as such:
 * MyCircularDeque obj = new MyCircularDeque(k);
 * boolean param_1 = obj.insertFront(value);
 * boolean param_2 = obj.insertLast(value);
 * boolean param_3 = obj.deleteFront();
 * boolean param_4 = obj.deleteLast();
 * int param_5 = obj.getFront();
 * int param_6 = obj.getRear();
 * boolean param_7 = obj.isEmpty();
 * boolean param_8 = obj.isFull();
 */

225.Implement Stack using Queues(用队列实现栈)(Easy)

Implement the following operations of a stack using queues.

  • push(x) – Push element x onto stack.
  • pop() – Removes the element on top of the stack.
  • top() – Get the top element.
  • empty() – Return whether the stack is empty.

Example:

1
2
3
4
5
6
7
MyStack stack = new MyStack();

stack.push(1);
stack.push(2);  
stack.top();   // returns 2
stack.pop();   // returns 2
stack.empty(); // returns false

Note:

  • You must use only standard operations of a queue – which means only push to back, peek/pop from front, size, and is empty operations are valid.
  • Depending on your language, queue may not be supported natively. You may simulate a queue by using a list or deque (double-ended queue), as long as you use only standard operations of a queue.
  • You may assume that all operations are valid (for example, no pop or top operations will be called on an empty stack).

解：想要用队列实现栈，常规想法可以使用两个队列，在每次出栈操作的时候，把元素临时保存到第二个队列中，在第一个队列还剩一个元素的时候把这个元素取出，从而实现类似栈的”后入先出”操作。

但是存在空间复杂度更优的方法，就是使用一个队列。具体操作方法是，每次入队都把整个队列循环弹出和新增元素，使得新添加的元素总在队列的前面，由此一来这个队列实际操作与栈无异。**关键步骤就是在于入队列时候的操作：queue.add(queue.remove())(remove()在队列为空的时候会抛出NoSuchElementException异常，poll()会返回null，其他没有区别)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class MyStack {

    Queue<Integer> queue;
    
    /** Initialize your data structure here. */
    public MyStack() {
        this.queue = new LinkedList<>();
    }
    
    /** Push element x onto stack. */
    public void push(int x) {
        queue.add(x);
        for(int i = 0; i < queue.size()-1; i++)
            queue.add(queue.remove());
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        return queue.remove();
    }
    
    /** Get the top element. */
    public int top() {
        return queue.peek();
    }
    
    /** Returns whether the stack is empty. */
    public boolean empty() {
        return queue.size() == 0;
    }
}

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */

232.Implement Queue using Stacks(用栈实现队列)(Easy)

Implement the following operations of a queue using stacks.

  • push(x) – Push element x to the back of queue.
  • pop() – Removes the element from in front of queue.
  • peek() – Get the front element.
  • empty() – Return whether the queue is empty.

Example:

1
2
3
4
5
6
7
MyQueue queue = new MyQueue();

queue.push(1);
queue.push(2);  
queue.peek();  // returns 1
queue.pop();   // returns 1
queue.empty(); // returns false

Notes:

  • You must use only standard operations of a stack – which means only push to top, peek/pop from top, size, and is empty operations are valid.
  • Depending on your language, stack may not be supported natively. You may simulate a stack by using a list or deque (double-ended queue), as long as you use only standard operations of a stack.
  • You may assume that all operations are valid (for example, no pop or peek operations will be called on an empty queue).

解：和之前用队列实现栈类似，可以用两个栈实现一个队列。但是由于栈只有一个出入口，所以不能用一个栈实现队列(队列中出队再入队可以实现倒置，栈不行).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class MyQueue {

    // 需要两个栈才能实现队列
    Stack<Integer> input;
    Stack<Integer> output;
    
    /** Initialize your data structure here. */
    public MyQueue() {
        input = new Stack<>();
        output = new Stack<>();
    }
    
    /** Push element x to the back of queue. */
    public void push(int x) {
        input.push(x);
    }
    
    /** Removes the element from in front of queue and returns that element. */
    public int pop() {
        peek();
        return output.pop();
    }
    
    /** Get the front element. */
    public int peek() {
        if(output.empty())
            while( !input.empty() )
                output.push(input.pop());
        return output.peek();
    }
    
    /** Returns whether the queue is empty. */
    public boolean empty() {
        return input.empty() && output.empty();
    }
}

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = new MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * boolean param_4 = obj.empty();
 */

239.Sliding Window Maximum(滑动窗口最大值)(Hard)

Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Return the max sliding window.

Example:

1
2
3
4
5
6
7
8
9
10
11
12
Input: nums = [1,3,-1,-3,5,3,6,7], and k = 3
Output: [3,3,5,5,6,7] 
Explanation: 

Window position                Max
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

Note:
You may assume k is always valid, 1 ≤ k ≤ input array’s size for non-empty array.

Follow up:
Could you solve it in linear time?

解：所有滑动窗口的题目，想到用队列解决。

方法一：暴力求解。枚举窗口的起点位置，因为窗口长度是k,所以枚举起点是0，终点是 length-1 。写一个二重循环，最后时间复杂度是O(n*k)。

方法二：这里用到单调队列(实际就是所谓的双端队列)，可以达到线性的时间复杂度。

双端队列可以操作队列里面的头元素和尾元素，一些API见下图：
JDK8 Deque API

我们通过双端队列维护的一个”单调队列”，从左到右为递减。所以每次对比元素都是peekLast()，弹出元素也是pollLast()

我们用双向队列可以在O(N)时间内解决这题。当我们遇到新的数时，将新的数和双向队列的末尾比较，如果末尾比新数小，则把末尾扔掉，直到该队列的末尾比新数大或者队列为空的时候才住手。这样，我们可以保证队列里的元素是从头到尾降序的，由于队列里只有窗口内的数，所以他们其实就是窗口内第一大，第二大，第三大…的数。保持队列里只有窗口内数的方法和上个解法一样，也是每来一个新的把窗口最左边的扔掉，然后把新的加进去。然而由于我们在加新数的时候，已经把很多没用的数给扔了，这样队列头部的数并不一定是窗口最左边的数。这里的技巧是，我们队列中存的是那个数在原数组中的下标，这样我们既可以直到这个数的值，也可以知道该数是不是窗口最左边的数。这里为什么时间复杂度是O(N)呢？因为每个数只可能被操作最多两次，一次是加入队列的时候，一次是因为有别的更大数在后面，所以被扔掉，或者因为出了窗口而被扔掉。(引用这篇文章)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
		
		if(nums.length == 0 || k <= 0) return nums;
		int len = nums.length;
		// 可以自己举个例子，推得这个result大小应该为len-k+1
		int[] result = new int[len - k + 1];
		// store index
		// 注意，dq用于保存数组下标
		Deque<Integer> dq = new ArrayDeque<>();
		for(int i = 0; i < len; i++) {
			//这里不需要循环，用一个判断就可 
			//因为我们最多只能在一轮中弹出一个超出范围的元素。（一轮我们只接受一个元素，所以我们最多弹出一个元素）。
			// dq 用于保存数组下标，这也是一个技巧
			if( !dq.isEmpty() && dq.peekFirst() == i-k) {
				// 双端队列中 poll() 相当于 pollFirst(),皮一下
				dq.poll();
			}
			
			// 新加入的元素必须比前面的小，否则前面比它小的元素都要出队
			while(!dq.isEmpty() && nums[i] >= nums[dq.peekLast()]) {
				dq.pollLast();
			}
			dq.offer(i);
			// dq是有序的，队列头总是最大的元素，只要下标在范围内，直接peek()即可
			if(i-k+1 >= 0) {
				result[i-k+1] = nums[dq.peek()];
			}
		}
		return result;
    }
}

时间复杂度：O(n)

空间复杂度：O(1)

621.Task Scheduler(任务调度)(Mid)

Given a char array representing tasks CPU need to do. It contains capital letters A to Z where different letters represent different tasks. Tasks could be done without original order. Each task could be done in one interval. For each interval, CPU could finish one task or just be idle.

However, there is a non-negative cooling interval n that means between two same tasks, there must be at least n intervals that CPU are doing different tasks or just be idle.

You need to return the least number of intervals the CPU will take to finish all the given tasks.

Example:

1
2
3
Input: tasks = ["A","A","A","B","B","B"], n = 2
Output: 8
Explanation: A -> B -> idle -> A -> B -> idle -> A -> B.

Note:

  1. The number of tasks is in the range [1, 10000].
  2. The integer n is in the range [0, 100].

解：

  1. 因为所有任务都是大写字母，所以可以申请大小为26的数组来保存任务类型个数。
  2. 对数组进行排序，按照出现的次数进行排序，优先记录出现次数多的任务。根据题意，时间至少为：retCount = (count - 1) * (n + 1) + 1 =>A->X->X->A->X->X->A(X为其他任务或者待命)
  3. 再排序下一个任务，如果下一个任务B个数和最大任务数一致，则retCount++ ==> A->B->X->A->B->X->A->B
  4. 如果空位都插满之后还有任务，那就随便在这些间隔里面插入就可以，因为间隔长度肯定会大于n，在这种情况下就是任务的总数是最小所需时间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int leastInterval(char[] tasks, int n) {
        // corner case
        if(tasks.length <= 1 || n < 1) return tasks.length;
        // 步骤1
        int[] counts = new int[26];
        for(int i = 0; i < tasks.length; i++) {
            counts[tasks[i] - 'A']++;
        }
        //步骤2
        Arrays.sort(counts);
        int maxCount = counts[25];
        int retCount = (maxCount - 1) * (n + 1) + 1;
        int i = 24;
        // 步骤3
        while(i >= 0 && counts[i] == maxCount) {
            retCount++;
            i--;
        }
        //步骤4
        return Math.max(retCount, tasks.length);
    }
}

其他参考题解：参考这篇文章

84.Largest Rectangle in Histogram(柱状图中最大的矩形)(Hard)

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

eg

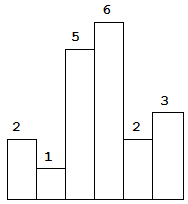
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

eg

Example:

1
2
Input: [2,1,5,6,2,3]
Output: 10

解：方法一：暴力法，枚举所有可能的柱子对。每次遍历的时候都基于当前的第i个柱子，向右用j扫描一遍。这样可以确保每一个都扫描扫过。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int largestRectangleArea(int[] heights) {
        // 方法一，暴力O(n^2)
        int maxArea = 0, len = heights.length;
        for(int i = 0; i < len; i++) {
            // 每次重新循环，minHeight都要更新
            int minHeight = Integer.MAX_VALUE;
            for(int j = i; j < len; j++) {
                minHeight = Math.min(minHeight, heights[j]);
                maxArea = Math.max(maxArea, minHeight * (j - i + 1));
            }
        }
        return maxArea;
    }
}
  • 时间复杂度：O(n^2)
  • 空间复杂度：O(n)

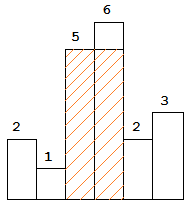
方法二，时间复杂度为O(n)的方法，利用Stack进行,具体来说，是一个单调栈。

它是怎么做的呢？

遍历的过程中，因为是从左开始遍历的，所以其实如果用一个有序的栈，其实是可以用O(1)得到某根柱子的左边界的。注意这里说的是左边界，右边界仍然需要遍历，因为右边还没遍历，没法一下子知道右边界。但是这是合理的，因为如果你不继续往右边界遍历，你永远也不知道右边界在哪里。

这个办法是维护一个栈，这个栈的元素是从小到大（对于栈，从小到大是从栈底到栈顶是从小到大排列的）进行排列的。因为这样排列，可以有效知道它的左边界在什么地方。

不得不说，这个算法需要后面不断反复地看，才能熟悉他它因为它的逻辑其实是比较复杂和精妙的。

栈的初始值为-1，也是巧妙的一点。

为了保证栈是从小到大的，每次入栈都进行一次判断， 必须比当前栈顶元素大，才能进栈，否则要把那个栈元素出栈。

进栈的时候要保留它的下标，因为后面计算的时候好计算它的宽度。

栈里面任何一个元素的左边界，都是它在栈里面的下一个元素。也就是说，如果一个元素要出栈了，它的左边界就是它在栈里的下一个元素，它的右边界就是比它小的那个元素，换句话说，哪个元素触发了另一个元素要被弹出栈，触发它的那个元素，就是被弹出元素的右边界。由此一来，当前被弹出元素的左边界和右边界都有了，通过公式计算得到的就是被以被弹出元素为中心能围成的最大矩形面积。

比如一个元素3，让9,5,4三个元素都出栈了，那么3就是9,5,4这三个元素的右边界

如果一个元素想要加入栈，但是它比栈顶元素要大，那么它不能是前一个元素的右边界，所以要把它保存到栈里面，直到下一个入栈的元素比栈里面它的上一个元素要小，那么开始出栈操作，因为找到了边界了。

扫描到哪里，谁更小，谁就是整个栈操作的颠覆者。

  • 实质是求每个柱子可以向左右两边延伸的距离
    • 向左：由于栈是单调递增的，因此以当前柱子为中心向左延展时，不能超过当前栈的上一个元素(最近的比它小的元素)
    • 向右：由于遇到非单调递增的元素时才开始弹出，所以当前位置的高度小于每个弹出的元素。因此，向右延展时，不能超过当前位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int largestRectangleArea(int[] heights) {
        // corner case
        if(heights == null || heights.length == 0) return 0;
        // 方法二，栈,O(n)
        // 主要目标是求能够覆盖当前第i个柱子的最大矩形，即为第i个矩形的"专属面积"
        Stack<Integer> stack = new Stack<>();
        // 栈里面存放heights数组的下标，取元素的时候为：heights[stack.pop()]
        stack.push(-1);
        int maxArea = 0, len = heights.length;
        for(int i = 0; i < len; i++) {
            // 只有遍历的heights[i]比当前stack里面的栈顶元素大，才能跳过while循环，直接入栈
            while(stack.peek() != -1 && heights[stack.peek()] >= heights[i])
                // 若当前遍历的heights[i]比栈顶元素小，则栈顶元素出栈，计算此时面积
                // 先pop()后peek()，很巧妙的写法设置
                // 这里多减一个1主要因为之前已经pop()了，这里要减回来
                maxArea = Math.max(maxArea, heights[stack.pop() ] * (i - stack.peek() - 1));
            stack.push(i);
        }
        // 如果遍历完了一遍最后栈不为空，则再用一重循环吧栈搞空
        while(stack.peek() != -1)
            maxArea = Math.max(maxArea, heights[stack.pop()] * (len - stack.peek() - 1));
        
        return maxArea;
    }
}
  • 时间复杂度：O(n)，n个数字每个会被压栈弹栈各一次。
  • 空间复杂度：O(n)，存放栈中元素。

85.Maximal Rectangle(最大矩形)(Hard)

Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing only 1’s and return its area.

Example:

1
2
3
4
5
6
7
8
Input:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
Output: 6

解：此题可以基于84题实现的找到矩形围成的最大面积来考虑，利用84题已经实现的函数，在遍历input的数组的时候将每一行值都记录，并且在有连续的1的时候进行累加(碰到0的话对应下标值要清空)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
    public int maximalRectangle(char[][] matrix) {
        if(matrix == null || matrix.length == 0) return 0;
        int cols = matrix[0].length, rows = matrix.length;
        int[] heights = new int[cols];
        int maxArea = 0;
        // 每次遍历之后都获取当前row的直方图，保存到heights中
        for(int i = 0; i < rows; i++) {
            for(int j = 0; j < cols; j++) {
                if(matrix[i][j] == '1') {
                    heights[j]++;
                } else {
                    heights[j] = 0;
                }
            }
            // 将当前直方图面积和之前最大面积进行比较，取一个最大值
            maxArea = Math.max(maxArea, largestRectangleArea(heights));
        }
        return maxArea;
    }
    
    public int largestRectangleArea(int[] heights) {
        // corner case
        if(heights == null || heights.length == 0) return 0;
        // 方法二，栈,O(n)
        // 主要目标是求能够覆盖当前第i个柱子的最大矩形，即为第i个矩形的"专属面积"
        Stack<Integer> stack = new Stack<>();
        // 栈里面存放heights数组的下标，取元素的时候为：heights[stack.pop()]
        stack.push(-1);
        int maxArea = 0, len = heights.length;
        for(int i = 0; i < len; i++) {
            // 只有遍历的heights[i]比当前stack里面的栈顶元素大，才能跳过while循环，直接入栈
            while(stack.peek() != -1 && heights[stack.peek()] >= heights[i])
                // 若当前遍历的heights[i]比栈顶元素小，则栈顶元素出栈，计算此时面积
                // 先pop()后peek()，很巧妙的写法设置
                // 这里多减一个1主要因为之前已经pop()了，这里要减回来
                maxArea = Math.max(maxArea, heights[stack.pop() ] * (i - stack.peek() - 1));
            stack.push(i);
        }
        // 如果遍历完了一遍最后栈不为空，则再用一重循环吧栈搞空
        while(stack.peek() != -1)
            maxArea = Math.max(maxArea, heights[stack.pop()] * (len - stack.peek() - 1));
        
        return maxArea;
    }
}
  • 时间复杂度：O(mn)。84题实现的函数的时间复杂度为O(n)，然后主函数有两个循环，但是因为内层循环和84题的函数是并列的，所以整个时间复杂度还是O(mn)

42.Trapping Rain Water(接雨水)(Hard)

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

42接雨水

The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!

Example:

1
2
Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6

解：本篇题解内容取材于这篇文章

方法一：按列求。

整个题目需要遍历heights的每一个元素，即每一列的值。而对于每一列，我们只需要关注当前列、当前列左边墙最高值、当前列右边墙最高值，关注这三个值。而且由于木桶效应，我们只需要看左边和右边最高值中的较小的那个即可，这样把当前左边与右边的最小值和当前列作比较，就能得出当前列能够最多盛多少水了。

按照题意，会有三种情况：

  1. 左边与右边两个中较矮的墙的高度大于当前列的墙的高度

此时用较矮的值减去当前高度，即为当前列能盛放的高度。

  1. 左边与右边两个中较矮的墙的高度小于当前列的墙的高度

此时当前列不能盛水。

  1. 左边与右边两个中较矮的墙的高度等于当前列的墙的高度

此时当前列也不能盛水。

所以，根据这三种情况写程序。外层循环遍历每一列，然后针对当前列求出这一列两边的最高的墙，并找出较矮的一端，和当前列高度比较，用上述这三种情况作为参考的结果即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int trap(int[] height) {
        // 方法一，按列求
        int sum = 0, len = height.length;
        //最两端的列不用考虑，因为一定不会有水。所以下标从 1 到 length - 2
        for(int i = 1; i < len-1 ;i++) {
            int maxLeft = 0;
            // 找出左边最高
            for(int j = i-1; j >= 0; j--) {
                if(height[j] > maxLeft) {
                    maxLeft = height[j];
                }
            }
            int maxRight = 0;
            // 找出右边最高
            for(int j = i+1; j < len; j++) {
                if(height[j] > maxRight) {
                    maxRight = height[j];
                }
            }
            // 找出左右两端更小的
            int min = Math.min(maxLeft, maxRight);
            // 根据之前分析，此时只有min大于height[i]，才能盛水
            if(min > height[i])
                sum += min-height[i];
        }
        return sum;
    }
}
  • 时间复杂度：O(n^2)，遍历每一列一遍需要O(n)，然后每次找出左边和右边最高的墙，加起来又需要一个O(n)，合在一起是O(n^2)
  • 空间复杂度：O(1)

方法二：动态规划

基于方法一的优化，在方法一中，我们要求当前每一列的左边界和右边界，都必须重新遍历一遍所有高度，其实可以优化的。

这里用maxLeft[]和maxRight[]两个数组，maxLeft[i]代表第i列左边最高的墙的高度，maxRight[i]代表第i列右边最高的墙的高度。注意，这里两个数组中定义的第i列的左边和右边，不包括i本身

递推公式：maxLeft[i]=Max(maxLeft[i-1], height[i-1])。它左边的墙的左边的最高高度和它左边墙的高度选一个作为最大的即可。这里相当于用到了”备忘录”，让之前的每一次遍历都有意义，都被记忆了。

类似的：maxRight[i] = Max(maxRight[i+1], height[i+1])。它右边墙的最高高度和它右边墙本身的高度进行比较，取最高的。

由此一来，就不需要像方法一那样，在内部又加了一层for循环，不用每次都去求一次i的左边和右边的最大值了，已经用两个数组分别记录好了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int trap(int[] height) {
        // corner case
        if(height == null || height.length < 3) return 0;
        int len = height.length, sum = 0;
        
        int[] maxLeft = new int[len], maxRight = new int[len];
        
        // 道理还是和之前一样，下标为0和len-1的两个地方一定没办法盛水，可以直接跳过
        for(int i = 1; i < len-1; i++) {
            maxLeft[i] = Math.max(maxLeft[i-1], height[i-1]);
        }
        for(int i = len - 2; i >= 0; i--) {
            maxRight[i] = Math.max(maxRight[i+1], height[i+1]);
        }
        // 把结果全部放入到maxLeft和maxRight之后，用下标统一遍历，用到了
        // maxLeft, maxRight, height三个数组
        for(int i = 1; i < len - 1; i++) {
            int min = Math.min(maxLeft[i], maxRight[i]);
            if(min > height[i]) {
                sum += min - height[i];
            }
        }
        return sum;
    }
}
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)，保存每一列左边最高边界和右边最高边界

方法三：动态规划在空间复杂度上的优化，双指针，时间复杂度为O(n)，时间复杂度为O(1)

动态规划中maxLeft[]和maxRight[]这两个数组中每个元素我们每次只用一次，之后不会再用，所以我们不需要用数组，用一个元素就够了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int trap(int[] height) {
        // corner case
        if(height == null || height.length < 3) return 0;
        // 方法三，双指针
        int maxArea = 0,leftmax = 0,rightmax = 0;
        int i = 0, j = height.length-1;
        while(i < j) {
            leftmax = Math.max(leftmax, height[i]);
            rightmax = Math.max(rightmax, height[j]);
            if(leftmax < rightmax) {
                maxArea += leftmax - height[i];
                i++;
            } else {
                maxArea += rightmax - height[j];
                j--;
            }
        }
        return maxArea;
    }
}

方法四：栈

这里用的，实际上在空间复杂度上不如方法三，但是用到栈的思路还是很巧妙的。

首先，这道题和括号匹配问题非常相似。我们可以每找到对应的两堵墙，就计算存储的水量，用栈保存每堵墙。

当遍历墙的高度的时候，如果当前高度小于栈顶的墙高度，说明这里会有积水，我们将墙的高度的下标入栈。

如果当前高度大于栈顶的墙的高度，说明之前的积水到这里停下，我们可以计算下有多少积水了。计算完，就把当前的墙继续入栈，作为新的积水的墙。

总体原则：

  1. 当前高度小于等于栈顶高度，将墙的下标值入栈，后移指针。
  2. 当前高度大于栈顶高度，出栈，计算当前墙和当前栈顶值的差值，为可存储的水量。然后用当前墙高度再和栈的新栈顶比较，重复两个判断，一直到当前墙的高度不大于栈顶高度或者栈为空，再把当前墙入栈，指针后移。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int trap6(int[] height) {
    int sum = 0;
    Stack<Integer> stack = new Stack<>();
    int current = 0;
    while (current < height.length) {
        //如果栈不空并且当前指向的高度大于栈顶高度就一直循环
        while (!stack.empty() && height[current] > height[stack.peek()]) {
            int h = height[stack.peek()]; //取出要出栈的元素
            stack.pop(); //出栈
            if (stack.empty()) { // 栈空就出去
                break; 
            }
            int distance = current - stack.peek() - 1; //两堵墙之前的距离。
            int min = Math.min(height[stack.peek()], height[current]);
            sum = sum + distance * (min - h);
        }
        stack.push(current); //当前指向的墙入栈
        current++; //指针后移
    }
    return sum;
}

394.Decode String(字符串解码)(Mid)

Given an encoded string, return its decoded string.

The encoding rule is: k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. Note that k is guaranteed to be a positive integer.

You may assume that the input string is always valid; No extra white spaces, square brackets are well-formed, etc.

Furthermore, you may assume that the original data does not contain any digits and that digits are only for those repeat numbers, k. For example, there won’t be input like 3a or 2[4].

Examples:

1
2
3
s = "3[a]2[bc]", return "aaabcbc".
s = "3[a2[c]]", return "accaccacc".
s = "2[abc]3[cd]ef", return "abcabccdcdcdef".

解：举个例子，s="3[a2[c]]"

这道题最后我们用StringBuilder记录目前为止字符的长度，然后需要用到两个栈进行辅助，分别是Integer和String泛型的栈，一个(numStack)用于保存当前字符重复的遍数,另一个(strStack)用于保存当前要重复的字符,需要它的原因是，哪怕你知道了某一个字符要重复的遍数，你还需要知道它前面还有什么字符，可能它前面的需要和它一起重复。

拿例子来说，走到了2[c]的时候，tail这个StringBuilder就是”c”，numStack就是2

具体入栈规则：

String泛型栈：每当遇到左括号的时候，要把之前记录的String(在StringBuilder里面保存着)都push到strStack，当然这个StringBuilder本身不会变化

Integer泛型栈：碰到数字就入这个栈，用来记录某一段字符串要重复的次数。

直到遍历到右括号，开始出栈。首先从numStack中pop()出一个数字，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
    public String decodeString(String s) {
        // 存储当前字符需要重复的遍数
        Stack<Integer> numStack = new Stack<>();
        // 记录前面没有数字的，"落单"的字母
        Stack<String> strStack = new Stack<>();
        // 记录迄今为止的解码结果
        StringBuilder tail = new StringBuilder();
        
        int n = s.length();
        
        for(int i = 0; i < n; i++) {
            char c = s.charAt(i);
            if(Character.isDigit(c)) { // 第一种情况，当前遍历的为数字
                int num = c - '0';
                // 因为前面的数字可能有十位、百位等，所以要循环判断
                while(Character.isDigit(s.charAt(i + 1))) {
                    // 每往后一位，num相当于要乘10再加上新数字
                    num = num * 10 + s.charAt(i + 1) - '0';
                    i++;
                }
                numStack.push(num);
            } else if(c == '[') { // 每当遇到左括号，就开始存encoded_string
                // 具体做法就是把当前tail的所有内容都push进strStack，然后重新定义一个StringBuilder记录
                // 被加密的内层的字符串
                strStack.push(tail.toString());
                // 清空tail
                tail = new StringBuilder();
            } else if(c == ']') {
                // 碰到右括号，首先把落单的，在被加密的字符的前面的字符pop出来
                StringBuilder temp = new StringBuilder(strStack.pop());
                // 记录当前被加密的内容的重复的次数，从numStack里面pop()即可
                int repeatedTimes = numStack.pop();
                // 解码的过程，持续将tail的内容放入到temp，从而变成："非加密+加密*次数"
                for(int j = 0; j < repeatedTimes; j++) {
                    temp.append(tail);
                }
                // 保存当前生成的temp值
                tail = temp;
            } else {
                tail.append(c);
            }
        }
        return tail.toString();
    }
}